Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Dynamique (Newton)

Posté par
mousse42 11-01-17 à 20:15

Bonjour,

1ère question :
Pour bien commencer un exercice, j'aimerai savoir si j'ai bien placé mes forces et bien posé mes équations .

2nd question :
Juste pour être sûr, ai-je le droit de dire que la somme des moments par rapport à n'importe quel point est nul. Le point B est-il le plus judicieux pour faire nos calculs?car le moment de \vec{T} et le moment de \vec{N} par rapport à B sont égals à \vec{0}.

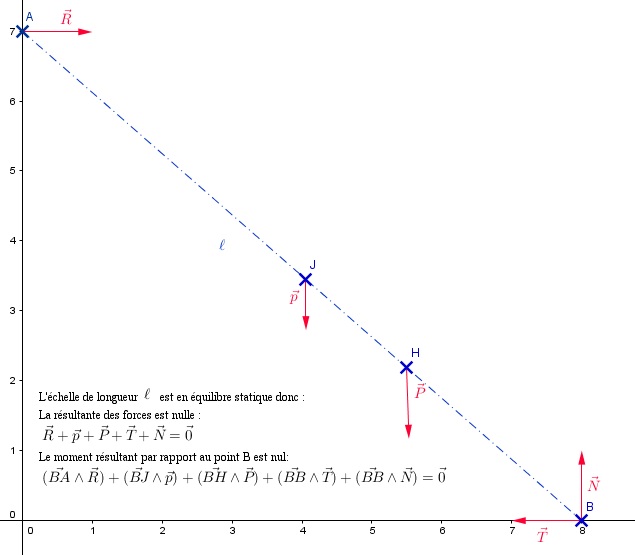
Le segment en pointillé, représente une échelle de longueur \ell

\vec{p} : poids de l'echelle, \vec{P} : poids de l'individu, \vec{R}, : Reaction du mur, \vec{N} : Réaction du sol, \vec{T} : Force de frottement.



Je vous remercie
mousse

Dynamique (Newton)

Posté par
vanoisere : Dynamique (Newton) 11-01-17 à 20:47

Bonsoir

Citation :
j'aimerai savoir si j'ai bien placé mes forces

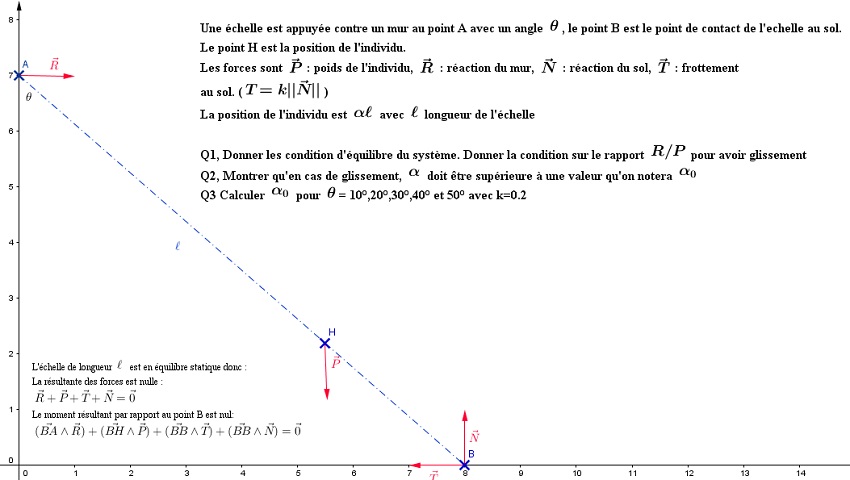
Tu ne fournis pas un énoncé complet... S'agit-il d'une échelle posé sur le sol le long d'un mur vertical sur laquelle un homme est immobile. S'il s'agit d'étudier l'équilibre de l'échelle, si on tient compte de frottements solides au sol et que l'on néglige les frottements au contact du mur, la réponse est oui.
Citation :
ai-je le droit de dire que la somme des moments par rapport à n'importe quel point est nul

oui en statique comme ici . Pas en dynamique bien sûr.
Citation :
Le point B est-il le plus judicieux pour faire nos calculs?

oui s'il s'agit de déterminer la réaction du mur. Le choix du point dépend de l'objectif de la question.

Posté par
mousse42re : Dynamique (Newton) 11-01-17 à 21:00

Merci vanoise,

Merci pour ces informations, je suis désolé, je n'ai pas encore d'énoncé complet, ou plutôt je travaille sur plusieurs exercices à la fois.

Avant, d'attaquer les questions, je voulais savoir mes forces étaient bien placées.

Merci et à très bientôt car je vais certainement tomber sur un os.

Posté par
vanoisere : Dynamique (Newton) 11-01-17 à 22:43

Ce que tu as déjà été capable de faire montre que tu domines déjà plutôt bien ton sujet !
Je te laisse réfléchir à tout cela et répondre aux questions posées. N'hésite pas à  demander une aide supplémentaire si tu le juges utile.

Posté par
mousse42re : Dynamique (Newton) 11-01-17 à 22:53

Bonsoir,

Pour la question 1,
les conditions d'équilibres sont :
La résultante des forces doit être nulle et le moment résultant doit être nul également.

La rapport R/P

Fixons comme référence le point B
\\ (\vec{BA} \wedge \vec{R}) +(\vec{BH} \wedge \vec{P}) +(\vec{BB} \wedge \vec{T}) +(\vec{BB} \wedge \vec{N}) =\vec{0} Or (\vec{BB} \wedge \vec{T}) +(\vec{BB} \wedge \vec{N}=\vec{0}

Donc on peut  considérer seulement :

(\vec{BA} \wedge \vec{R}) +(\vec{BH} \wedge \vec{P}) =\vec{0}

Et à partir de là, je déduis que \dfrac{R}{P}=\alpha \tan \theta

Et là je bloque car je n'arrive pas à interpréter ces résultats

Dynamique (Newton)

Posté par
mousse42re : Dynamique (Newton) 12-01-17 à 00:12

La condition : T=k||\vec{N}|| veut dire que le système est sur le point de glisser

Par contre , il est dit que pour que ça ne glisse pas, il faut que ||\vec{T}||\leq k||\vec{N}|| (je fais référence à mon cours)

Citation :
Dans cet encadré, c'est ce que je ne comprends pas Ce n'est pas une citation


Or la norme de \vec{N} est égal à la norme de \vec{P}

Et dire que ||\vec{T}||\leq k||\vec{N}||, se traduit par : plus la force de frottement \vec{T} est faible et moins le système glisse. Or \vec{T} est de sens opposé au glissement.

Il y a un truc que je ne saisi pas...

Admettons qu'il y ait glissement :

||\vec{T}||> k||\vec{N}|| et puisque R=T et que P=N, on a

\dfrac{R}{P}>k \implies \dfrac{R}{P}=\alpha \tan \theta>k

Conclusion si \alpha \tan \theta>k il y a glissement.

Voilà pour la première question, avec beaucoup de mal !!

Question 2

Valeur \alpha_0
Pour qu'il y ait glissement

\alpha \tan \theta>k \implies \alpha> \dfrac{k}{\tan\theta}
On note donc la valeur \alpha_0=\dfrac{k}{\tan\theta}

Question 3

\left( \begin{array}{c|ccccc}\theta & 10° & 20° & 30° & 40° & 50° \\ \hline \alpha_0 &1.35&0.55&0.35 &0.24&0.17 \end{array} \right)

Interprétation pour \theta = 10°, on peut se promener sur toute la longueur de l'echelle, et seulement un peu plus de la moitié si l'angle et de 20°.

Exercice terminé. Par contre je ne comprends pas pourquoi, je n'ai pas le poids de l'individu quelque part.

Je reviendrai demain.

Posté par
mousse42re : Dynamique (Newton) 12-01-17 à 15:01

Bonjour

Puisque je n'ai plus aucun signe, faut-il sous-entendre que ce que j'ai fait est juste ?

J'en doute un peu. J'ai du mal à croire qu'une mouche puisse faire glisser l'echelle si elle se balade au délà du quart de la longueur de l'échelle (pour \theta =40°)

Mais, le fait que l'échelle soit de masse nulle, pourrait peu être expliquer cet étrange phénomène.

à+
mousse

Posté par
vanoisere : Dynamique (Newton) 12-01-17 à 16:13

Bonjour
Tu as bien travaillé. Je viens de reprendre les différentes étapes de ton raisonnement : je suis d'accord avec tout ce que tu as écrit.

Citation :
Par contre je ne comprends pas pourquoi, je n'ai pas le poids de l'individu quelque part

Parce que le poids de l'échelle est négligeable (ou au moins négligé...). Dans ce cas, N et T sont deux forces d'intensités proportionnelles à P : modifier le poids dans ces conditions ne modifie pas le rapport T/N qui intervient dans la loi de Coulomb.
Citation :
J'en doute un peu. J'ai du mal à croire qu'une mouche puisse faire glisser l'echelle si elle se balade au délà du quart de la longueur de l'échelle (pour \theta =40°)

Tu as évidemment raison ! La modélisation faite ici n'a de sens que si le poids de la charge  est très supérieur à celui de l'échelle. A la rigueur, cela est envisageable avec un homme mais avec une mouche !
Pour rendre l'exercice plus réaliste, il faudrait, comme ton schéma le suggère, tenir compte du poids p de l'échelle ; imaginer par exemple une personne de 70kg grimpé sur une échelle de 15kg... Je suis sûr que tu saurais résoudre ce problème !

Posté par
mousse42re : Dynamique (Newton) 12-01-17 à 17:12

Salut vanoise et merci pour tes commentaires.

Pour ce nouveau problème,  j'ai deux trois bricoles à terminer et je m'y attèle de suite.

à+

Posté par
mousse42re : Dynamique (Newton) 12-01-17 à 21:15

Dans le premier cas le point H (individu) était le centre de gravité du système.

Soient H', le nouveau centre de gravité, G le centre de gravité de l'échelle . M la masse de l'individu (70kg) et m la masse de l'echelle 15kg.

\vec{BH'}=\dfrac{1}{M+m} (M.\vec{BH}+m.\vec{BG})=\dfrac{1}{M+m} \left(M(-\alpha \ell \sin \theta _x +\alpha \ell \cos \theta _y) + m(-\dfrac{\ell}{2}\sin \theta _x+\dfrac{\ell}{2}\cos \theta _y)\right)

\vec{BH'}=\dfrac{\alpha M +\frac{m}{2}}{M+m} (-\ell \sin \theta _x+ \ell \cos \theta _y) \quad =\quad \dfrac{\alpha M +\frac{m}{2}}{M+m} . \vec{BA} \quad = \quad \varphi(\alpha) . \vec{BA}

avec \varphi(\alpha)= 0.83\alpha +0.088

Or :  \varphi(\alpha)\tan \theta>k \implies \alpha>\dfrac{k}{0.82\tan \theta}-0.107  donc on note   \alpha'_0 =\dfrac{k}{0.82\tan \theta}-0.107



\left( \begin{array}{c|ccccc}\theta & 10° & 20° & 30° & 40° & 50° \\ \hline \alpha_0 &1.35&0.55&0.35 &0.24&0.17 \\ \hline \alpha'_0 &1.26&0.55&0.31 &0.18&0.10\end{array} \right) \\

Peut-on conclure que plus l'echelle est massive et plus c'est dangereux??

Dans le cas où mes calculs sont justes.

Merci

Posté par
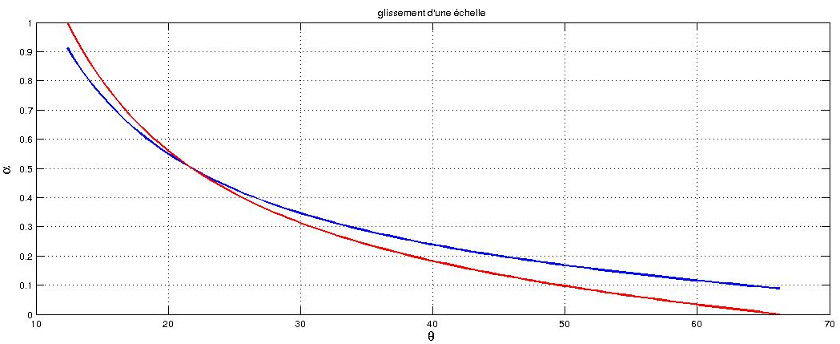
vanoisere : Dynamique (Newton) 12-01-17 à 23:21

Tu es réactif ! D'accord avec tes calculs littéraux. Je pense en revanche qu'il y a erreur dans ton tableau de valeurs. Tu trouveras ci-dessous les courbes représentant les variations en fonction de de o (en bleu) et de 'o (en rouge).
Les deux courbes se coupent pour =0,5 : logique : dans ce cas, les points H et J sont confondus : les poids de l'échelle et de l'homme de la seconde modélisation ont la même influence sur l'équilibre que le poids d'un homme de 85kg situé au milieu de l'échelle dans le premier modèle. Ce nouveau modèle a le mérite de rendre compte d'un fait expérimental simple : si le bas de l'échelle est trop écarté du mur (ici 67° environ), l'échelle glisse sous l'action de son propre poids sans personne de grimpé dessus...

Citation :
Peut-on conclure que plus l'echelle est massive et plus c'est dangereux

Il faut nuancer...
Si l'échelle est peu écarté du mur : <21,8° (situation correspondant à =0,5) le poids de l'échelle augmente proportionnellement davantage  N que T : l'échelle a moins tendance à glisser.
Si l'échelle est très écarté du mur : >21,8° , le poids de l'échelle augmente proportionnellement davantage T que N : l'échelle glisse plus facilement.
Remarque : cet exercice a l'intérêt de faire réfléchir aux influences des différents paramètres du dispositifs. En pratique, les "pieds" de l'échelle sont le plus souvent garnis de patins en caoutchouc, ce qui augmente fortement la valeur de k et minimise les risques de glissements...

Dynamique (Newton)

Posté par
mousse42re : Dynamique (Newton) 12-01-17 à 23:44

vanoise, un grand merci pour avoir vérifié mon travail.

Je vais regarder les valeurs de \alpha'_0 demain .
Je bloque sur un autre problème de physique.

Merci et à bientôt


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !