Inscription / Connexion Nouveau Sujet
Dynamique et frottements
Salut à tous, je révise de vieux exos de dynamique en vue d'un DS final et je bloque sur l'un d'entre eux. Je vous mets l'énoncé ci-dessous :
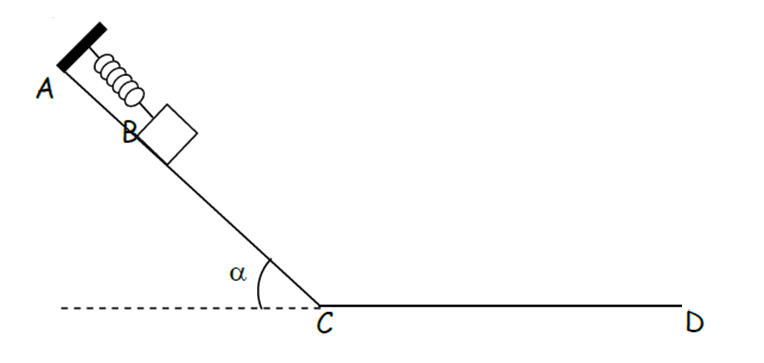
La figure ci-dessous représente une piste (ABCD) de longueur BC=2m, inclinée d'un angle α=25° par rapport à un tronçon horizontal CD=0.2m. Une masse m, assimilée à un point matériel, est placée en contact avec l'extrémité libre B d'un ressort de constante de raideur k=15N/m et de longueur à vide l0. On supposera dans tout le problème que les frottements entre la masse m et la piste (ABCD) sont caractérisés par des coefficients μs=0.6 (statique) et μg=0.4 (dynamique).
Le ressort étant comprimé de x1=10 cm, déterminer la vitesse de la masse m = 0,4 kg au point D en ms-1. On aura une précision de 1/100.
En fait le problème vient du fait que je ne sais pas trop d'où partir. J'ai essayé avec le théorème de l'énergie cinétique et avec celui de la conservation de l'énergie mécanique mais je ne trouve rien de concluant..
En plus, je ne comprends pas bien comment "s'utilisent" les forces de frottements.
Si vous aviez des propositions pour me débloquer un peu, je suis preneur ! 
D'ailleurs, je peux détailler ce que j'ai fais pour le théorème de l'énergie cinétique :
 Ec =
Ec =  W(
W( F
F
Or vB = 0
Donc on a 1/2 m*(vD)2 = W(P)+W(Fr) + W(Ff)
où Fr est la force du ressort et Ff la force de frottement.
On a : W(Ff) =  d * R * BC +
d * R * BC +  d * R * CD
d * R * CD
W(Fr) = ... Je ne sais pas comment exprimer la valeur du travail en sachant que la force est de la forme k*(x1-l0)
Et le poids ne travail qu'entre B et C donc W(P) = P * BC * cos( /2 -
/2 -  )
)
J'en suis là..
La configuration du problème est un peu invraisemblable. La façon dont le ressort contribue au mouvement au-delà du point C en particulier n'est pas claire... (son action reste-t-elle parallèle à la piste ?)
Utiliser le théorème de l'énergie cinétique est une bonne idée.
Il faut cependant garder en tête que les forces de frottements s'opposent au mouvement et que leur contribution au travail des forces extérieures sera donc négative.
Les forces de frottements s'obtiennent en multipliant le coefficient de frottement par la composante normale (à la piste) du poids : il faudra distinguer les deux tronçons BC et CD.
Le travail du ressort s'obtient simplement par intégration :
-
où désigne la distance au point B...
Merci pour les conseils 
Etant donné que j'ai la réponse, je vais essayer plusieurs possibilités pour voir laquelle est la bonne...
J'ai juste une autre question :
On est d'accord que le Poids ne travaille qu'entre B et C ?
D'où W(P) = P*BC*cos( /2 -
/2 -  ) ?
) ?
Oui, c'est correct.
Reste que le poids intervient aussi dans l'expression des forces de frottements, et ce aussi bien entre B et C qu'entre C et D.
Pour les forces de frottements j'ai :
WB C (Ff) =
C (Ff) =  d * R * BC = -mg
d * R * BC = -mg *BC*cos(
*BC*cos( )
)
Et R = -mg*cos( )
)
Et WC D (Ff) = -
D (Ff) = - d * mg * CD
d * mg * CD
C'est correct ?


