Inscription / Connexion Nouveau Sujet
Dynamique équilibre statique
Bonsoir j'ai une exercice à faire et j'ai du mal à le réaliser si quelqu'un peut m'aider.
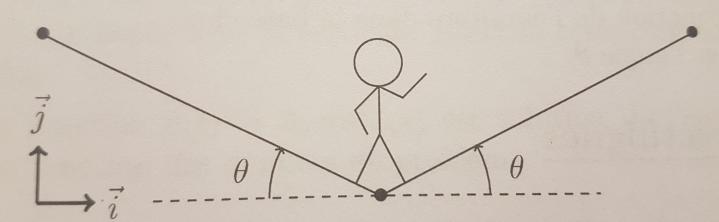
Lors de ces péripéties, Indiana Jones se retrouve au milieu d'un pont de lianes. Pour simplifier, on considérera le pont comme une corde attachée à deux poteaux fixes et Indiana Jones sera considéré comme une masse ponctuelle (m=70 kg) placée au milieu de la corde.
1. Refaire le schéma et représenter les forces appliquées à Indiana Jones : son poids P(vecteur) et la tension du pont de liane T1(vecteur) à gauche et T2(vecteur) à droite.
2. Comme Indiana Jones est au milieu du pont, par symétrie, l'angle
entre le pont de liane et l'horizontal est identique des 2 côtés. exprimer les composantes de ces forces dans la base (
: 
) en notant ||T1|| et ||T2|| les normes de T1(vecteur) et T2(vecteur). On représentera les réponses sous la forme :
Px= T1x= T2x=
Py= T1y= T2y=
3. En appliquant le principe fondamental de la statique selon l'axe
montrer que T1(vecteur) et T2(vecteur) ont la même norme, que l'on notera ||T||.
4. En appliquant le principe fondamental de la statique selon l'axe , déterminer en fonction de l'angle 
et de la masse m de notre héros, la tension ||T|| de chacun des deux brins de l'accord de nécessaire pour le maintenir en équilibre.
5. Pour un angle réaliste de = 10, calculer la valeur numérique de ||T||.
6. Quel est la limite de cette force quand tend vers π/2 ? on donnera d'abord l'expression littérale de ||T||, puis on calculera sa valeur numérique en prenant g= 9,81m.s^-2.
7. Quelle est la limite lorsque tend vers 0 ? Peut-on faire sécher sa serviette sur une corde à linge parfaitement horizontale ? justifier.
La première questio'jai pas de soucis mais pour la deux je voulais vérifier déjà que Px=0
Py=-mg
T1x=sinx
T1y=-cosy
T2x=cosx
T2y=siny
Merci de votre aide d'avance.
Bonjour
Bien sûr : Px=0 ; c'est le "b a ba " des cours de maths de l'enseignement secondaire !
OK pour Py mais le reste est faux. Je te corrige un seul cas et tu adapteras pour les autres :
Que viennent faire les “x” et les “y” dans les expressions des coordonnées des vecteurs forces ?
Donc si je comprend
T1x= ||T1||.sin
T2x= ||T2||.cos
T2y=||T2||.sin
?
Et pour te répondre je voulais me repérer et j'ai placer les x et y comme je fesais pour la cinétique 😅 ...
Apres pour la question 3 c'est T1+T2+P=0 ?
Pour x) T1x+T2x+Px=0
||T1||.sin+||T2||.cos+0
Pour y) T1y+T2y+Py=0
-||T1||.cos+||T2||.son-mg
Est ce cela ?
Je réécris toutes les relations car je viens de m'apercevoir que j'ai fait une erreur de frappe sur un indice qui t'a peut-être induit en erreur. Désolé !
Ah okey vous inquiétez pas je n'avais pas remarquer qu'il y allais avoir un soucis après.
Du coup pour la 3 c'est la formule que j'ai utiliser Px+T1x+T2x
= 0-||T1||x cos +||T2||xsin
Et py+T1y+T2y=-mg+||T1||xsin+||T2||x sin
?
Tu n'as pas tenu compte de mon dernier message...
Cela conduit de façon immédiate, dans la mesure où le cosinus est différent de zéro, à :
Cela répond à la question 3.
Projection de la relation fondamentale de la statique sur l'axe vertical :
En tenant compte de l'égalité précédente, cela donne simplement T en fonction de m.g et de . Cela répond à la question 4.
Je te laisse continuer...
Normalement c'est pour le 5
T1= -||T1||x cos / ||T2||x cos
=cos(10)/cos(10)
=-1
T2= -mg+||T2||sin / ||T2||sin
= -mg + sin (10) / sin (10)
= 1
T=1-1=0
C'est cela ?
As-tu bien compris mes messages précédent ? Tu as vraiment écrit n'importe quoi dans ton dernier message.
La question 4 conduit à :
Enfin si je comprend
Py+T1y+T2y=0
||P||+||T1||sin+||T2||sin =0
-mg+(||T1|| + ||T2||)sin =0
||T||= -mg/2sin
Je t'ai fourni une démonstration détaillée. Reprend la en faisant attention aux signes. La norme d'un vecteur ne peut pas être négative !
Oui pardon c'est mg/2sin
À part le signe moin qui disparaît le raisonnement est juste ?
Py+T1y+T2y=0
||P||+||T1||xsin +||T2||x sin=0
mg+(||T1||+||T2||)sin=0
Sachant que ||T1||+||T2||= ||T||
||T||= mg/2sin
À ma deuxième formule ou je dis mg + (||T1||+||T2||) sin =0 je m'est -mg et quand je dit que ||T|| = mg/2sin jenleve le moin ?
Je le poste en supérieur car c'est se que j'apprends et j'ai pas fais de bac s j'ai fait un bac technologique st2s j'ai pas les bases dans ces matières... Désolé
Mais j'ai exactement repris ce que vous avez écrit sauf que je les pas mis dans le même sens je doit pas comprendre ce que vous me demandiez
-mg +||T1||sin + ||T2||sin = 0
Mais c'est bien égale à mg/2sin
Okay mais donc par rapport à ce que j'ai fais je sais que ||T1||+||T2||= ||T||
Donc ||T||=mg/2sin
Après la question 5 je remplace par 10
Dans la question 6 je remplace par π/2
Et dans le 7 je remplace par 0 mais dans le 7 il y a un truc avec l'infinie je crois ?
Avant de faire un calcul, il faut réfléchir à la situation physique. Le poids est compensé par les deux composantes verticales des tensions. Si le fil devient horizontal, ces deux composantes verticales n'existent plus. Il est donc impossible d'avoir un fil horizontal, c'est à dire d'avoir =0.
Mathématiquement, on constate que plus se rapproche de zéro, plus la norme T devient grande et la limite mathématique de T quand tend vers zéro est effectivement l'infini, ce qui montre bien que cette situation est impossible. D'ailleurs pratiquement, dès que T dépasse une certaine valeur, le câble casse !
Annuler
connectez vous