Inscription / Connexion Nouveau Sujet
Dynamique du point
Bonjour a tous,
J'ai actuellement quelques problemes avec mon exercice de physique, qui est :
Un balancier OA est constitué d'une tige de longueur l, de masse négligeable et d'une masse m située à son extrémité en A. Cette dernière est considérée comme ponctuelle.
Ce balancier peut tourner autour d'un axe Oz. On pose (en vecteurs) (Ox,OA) = theta
Un ressort est placé en O. elui-ce exerce sur le balancier un couple de rappel vecteur(N) = -C*theta*vecteur(k)
1) Quelle est la dimension de C ?
2) Faire un schéma représentant les forces et les moments agissant sur le balancier. Sans résoudre, donner les conditions d'équilibre.
3)Si l'axe OA passe d'une position (theta) à la position (theta+dtheta), calculer les travail élémentaire associé à ce déplacement.
4) Montrer que ce travail élémentaire est une forme différentielles exacte et que l'on peut définir une énergie potentielle Ep composée de deux termes que l'on identifiera. La calculer sachant que Ep=0 pour x=0.
5) Tracer le graphe représentant cette énergie potentielle pour variant de -pi/4 à pi/4 et déterminer graphiquement les positions d'équilibre. Étudier la stabilité de ces positions d'équilibre sachant que C = 0.97*10^-2 SI, m = 10m/s², l=10cm.
6)Calculer le moment cinétique du balancier
7)À partir du théorème du moment cinétique, calculer la période T des oscillations lorsque le balancier oscille autour de l'une de ses positions d'équilibre stable. On posera theta=theta(indice e) + ε,
T = f(m,g,l,C, theta(indice e)).
J'ai trouve pour la premiere et la deuxieme question mais je ne sais pas comment m'y prendre pour la 3eme, pourriez vous m'aider s'il vous plait ?
Merci d'avance,
2) Faire un schéma représentant les forces et les moments agissant sur le balancier. Sans résoudre, donner les conditions d'équilibre.
qu'as-tu fait?
Donc j'ai dis qu'il y a avait :
J'ai pris comme systeme { masse + fil }
Il y a donc comme force : le poid P de la masse(le poid du fil etant negligeable, il ne va donc pas rentrer en compte), la reaction du support en O et enfin un couple de moment.
Oups desole pour le double post(je ne sais pas comment modifier mon message)
Condition d'equilibre : somme des forces = 0 et somme des moments = 0
on te demande un schéma:
Condition d'equilibre : somme des forces = 0 et somme des moments = 0
donc ici:
P + R = 0 (vecteurs en gras)
et ...
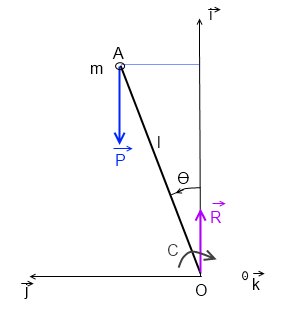
Oui c'est ce que j'ai fait. Mais je bloque du coup a la question 3... comment calculer le moment d'un couple ?
Je pense avoir trouver pour la question 3,
Par definition dW(vect(F)) = vecteur(F).d(vect(l)) ou encore dans le cas d'une rotation ca sera dW(vect(F)) = Nd(theta) ou N est le moment de la force f par rapport a un axe. (Nb : Ici d est un d rond et pas droit, on a pas encore suppose qu'il s'agisssait d'une differentielle exact)
Donc j'obtiens, dW(vect P) = mgsin(theta)l.d(theta)
dW(vect R) = 0(ca coupe l'axe Oz)
dW(vect N) = -C*(theta).dtheta (cf enonce)
d'ou finalement dW(F resultante) = (mgsin(theta)l-C*theta)).dtheta
Est ce correct ?
Mais comment faire la question 4 ? Je sais que si cela est une differentielle exact( et c'est le cas car il n'y a qu'une seule variable)
On a d(W) = -dEp ... Mais apres ?
Un ressort est placé en O. celui-ci exerce sur le balancier un couple de rappel vecteur(N) = -C*theta*vecteur(k)
donc le moment du couple par rapport à O, c'est N
donc ici, à l'équilibre,en prenant les moments par rapport à O:
N + M P/O = O (vecteurs)
3) oui c'est ça (tu t'es bien rattrapé, j'ai cru un moment que tu ne savais pas ce qu'était un couple de rappel 
W = -C
d +mgl sin d
Du coup, ici N vaut -mgsin(theta)l et non -C*theta ?
mais non, le couple de rappel est le moment N = -C
k (par rapport à O)
il n'a rien à voir avec le moment de P par rapport à O
en revanche à l'équilibre tu as : N + M P/O = 0 ( car R a un moment nul par rapport à O)
Merci bien !
Maintenant pour la question 4)
On a donc brillamment (ou pas) trouve que W = -Cd+mglsind
or on a dW = W (en effet, forme differentielle exact car il n'y a qu'une variable)
et dEp = -dW
d'ou Ep = -mglcos + C2/2 + cst
or pour =0 on a Ep = 0
d'ou cst = mgl
Ce qui about a Ep = -mgl(cos-1) + C2/2
Est ce correct ?
c'est presque ça:
on a dW =
W (en effet, forme differentielle exact car il n'y a qu'une variable)non, si tu as une seule variable, la différentielle est totale, mais pas forcément exacte.
par ex. le travail
W des forces de frottements n'est pas une différentielle exacte (même si le mouvement ne dépend que d'une variable)
ici on cherche une fonction Ep(
) qui vérifierait : dEp = -W
dEp = C
-mgl sin
donc on trouve finalement (en tenant compte de la convention Ep(0) = 0) que la fonction suivante convient:
Ep = C
2/2 + mgl(cos-1)
donc
W est une forme différentielle (totale) exacte car on a trouvé Ep()
W = dW = -dEp
sauf erreur
D'accord, merci bien.
Effectivement j'ai fait quelques erreurs de signe.
Concernant le moment cinetique, on sait par definition que 
o = vect(OM)^vect(v)m
Mais je ne vois pas comment faire dans ce cas, car OM varie non ?
4) tu n'as pas complètement répondu:
...et que l'on peut définir une énergie potentielle Ep composée de deux termes que l'on identifiera.
5) je trouve 3 positions d'équilibres dont 2 stables
6) le moment cinétique du balancier est celui de A puisqu'on néglige la masse de la tige.
Ha je pensais que c'etait d'une part C2/2 et d'autres part mgl(cos-1)
.. Comment faut-il s'y prendre alors s'il vous plait ?
Ha excusez moi ( je n'ai pas vu votre message),
et bien je ne vois pas quelle autre type d'energie.. car nous n'avons pas d'elastique la non ?
Malheureusement, meme en cherchant je ne vois pas de quoi il s'agit :/
Mais en tracant la courbe, je trouve une parabole, est ce normal ?
car nous n'avons pas d'elastique la non ?
nous avons un ressort spiral donc de l'énergie potentielle élastique
sauf qu'ici on a un couple de rappel (un moment) de la forme -k
au lieu d'une force de rappel F = -k
xHa d'accord, merci beaucoup !
Cependant lorsque je trace la courbe
http://www.wolframalpha.com/input/?i=-0.0010*sin%28x%29%2B0.0079*x
Je ne trouve pas de minimum ni de maximum...
peux-tu redonner les constantes, il y a qqchose qui colle pas plus haut:
C = 0.97*10^-2 SI, m = 10m/s² (!!!) , l=10cm.
C'est bon je viens de trouver.. en fait(j'ai fait une erreur de frappe)
C = 0,79*10^-2
http://www.wolframalpha.com/input/?i=-0.010*sin%28x%29%2B0.0079*x
5) Ep() = C2/2 + mgl(cos - 1)
Ep = C/2 ( 2 + 2mgl/C (cos - 1) )
avec C = 0,79*10^-2 USi, m=10g l=10cm et g=10m/s2 on trouve
Ep = C/2 ( 2 + 2.54 (cos - 1) )
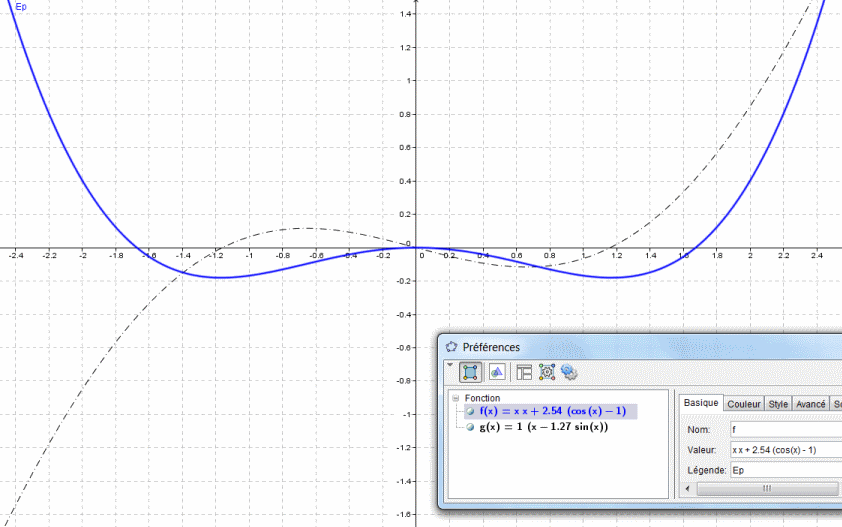
on trace la fonction: f(x) = x2 + 2.054 (cosx - 1)
et aussi x -1.27sin(x) pour bien repérer les extrema.
je trouve: e = +/- 1.16 rad
Bonjour,
Merci encore pour ton aide, mais ne faut-il pas tracer -dEp/dx pour reperer les extremums ?
Ha excusez moi, j'ai mal lu votre message..
Oui, j'obtens a peu pres la meme chose.
Pour 6)
o=OM^mv=OA^mv
or v = ld d'ou
OA^mv = l^ld=l2dk ?
le problème, ici, est que Ep a une valeur très faible .
j'ai donc "zoomé" en représentant kEp et kE'p car les extréma de f et de k.f sont les mêmes
donc je trace: f = Ep / (C/2) et g= E'p/C pour y voir qqchose
mais si tu peux t'arranger pour tracer Ep directement, alors c'est parfait.
Oui c'est cela.
Merci beaucoup pour l'aide que tu m'accordes en tout cas !
Par contre, il y a quelque chose qui me derange dans la 7eme question, on me parle de l'un de ses positions stables.. mais n'y en a t-il pas qu'une seule puisque -1.16rad n'est pas plutot une position d'equilibre instable ?
Étudier la stabilité de ces positions d'équilibre sachant que C=...
d'après la courbe de Ep, tu trouves combien de positions d'équilibre?
J'ai trace -dEp et je trouve 2 endroits ou la tangente s'annule on va dire donc 2 positions d'equilibre
j'ai tracé la dérivée en pointillés plus haut, et elle s'annule en 3 points
de plus on voit bien que Ep a 3 extréma , en +1.16 en -1.16 et en ...
Mais il ne s'agit pas plutot de savoir les extremums de la fonction derive et non la fonction Ep pour connaitre les positions d'equilibre ?
ah non, les positions d'equilibre correspondent aux extrema de Ep
vérifie dans ton cours.
ou encore aux points annulant la dérivée de Ep (ici / dEp/d=0)
les positions stables sont les minima de Ep
les positions instables sont les maxima de Ep
J'ai une question concernant mes graphes. J'obtiens deux courbes nettement differentes pourtant je pense avoir entrer la meme formule..
bonsoir,
ce ne sont pas les mêmes fonctions mais elles se ressemblent puisque c'est Ep et 2/C Ep si je ne m'abuse.
la 2ème semble correspondre à Ep
mais tu as encore changé C, maintenant c'est 0.72 10-2 USI (??)
tu as du mal à recopier les énoncés
Euh oui excusez moi c'est bien 0.79*10^-2...
Mais alors laquelle des deux est correct ?
Dans la premiere j'ai trace f(x) = mgl(cos(x)-1)+Cx2/2
et dans la deuxieme j'ai trace f(x) = (mgl2/C)*(cos(x)-1)+x2
J'ai l'impression d'etre revenu en primaire tout d'un coup..
Ou est l'erreur ?
Merci encore pour votre aide,
Olala je viens tout juste de comprendre !
Dans la premiere j'ai trace la courbe donnant Epp+Epl ..
(desole encore pour le double post)
5) Tracer le graphe représentant cette énergie potentielle
on a trouvé:
Ep = C/2 (
2 + 2mgl (cos - 1) )
donc c'est cette fonction qu'on trace
(j'ai tracé 2/ C Ep car je n'arrivais pas à tracer Ep correctement ,je ne voyais rien ;-( alors j'ai rusé, mais toi tu y arrives très bien apparemment
Donc c'est la 2eme qu'il faut garder alors... mais je ne vois pas en quoi ces deux fonctions ne sont pas equivalentes.
elles sont identiques à une constante multiplicative près
Ep
2/C Ep = 278 x Ep c'est juste un facteur d'échelle qui les distingue
tu peux aussi tracer 1000 Ep (du moment que tu l'indiques bien sur ton graphe dans la légende (Ep ou 1000 Ep ou 50 Ep ou ...)
pour les extréma ça ne change rien.
Annuler
connectez vous