Inscription / Connexion Nouveau Sujet
Dynamique de Rotation du Solide (poulie)
Bonjour,
Je suis en train d'étudier la dynamique des solides en Italie et je dois dire que ça me pose parfois un peu problème !
J'ai un exercice en particulier sur une poulie que j'ai du mal à résoudre. C'est un défaut de méthode je pense.
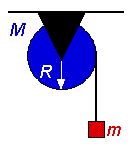
On a donc un disque homogène de rayon 0,5 m et de masse 20 kg qui peut tourner librement autour d'un axe horizontal fixe passant per son centre et reposant sur deux appuis. Une corde enroulée sur le bord du disque a une masse de 1 kg à son extrémité. Dans l'hypothèse que la corde ne glisse pas sur le disque, calculer les modules de l'accélération angulaire du disque et de l'accélération linéaire du corps lié à au disque.
J'ai compris le lien entre l'accélération linéaire de la masse et l'acc. angulaire du disque mais je n'arrive pas à trouver l'acc. angulaire du disque !
Je sais que le moment total des forces calculé au centre de gravité du système est égal au moment d'Inertie * l'acc. angulaire
dK/dt = M(centre gravité) = I*dw/dt
Mon problème est que j'imagine que le CG n'est pas le centre du disque à cause de la masse qui le déplace ? Mais comment le calculer car on sait pas à quelle longueur de la corde se trouve la masse ?
Du coup, le centre d'Inertie non plus, n'est pas celui d'un disque homogène à cause de cette masse, non ?
Si je pouvais avoir un petit coup de pouce, je devrais m'en sortir pour la suite 
Merci beaucoup !
avec un dessin pour illustrer..
Edit Coll : image placée sur le serveur de l' 
Merci d'en faire autant la prochaine fois ! 
Bonjour Miniminette,
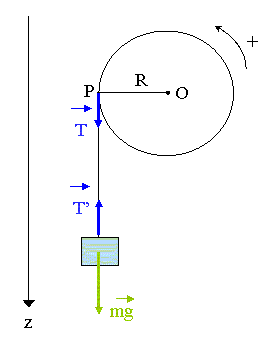
voici le petit coup de pouce attendu. Refere-toi a la figure ci-dessous : Sur ton schema il faut rajouter la tension de la corde, pour celle appliquee au centre de gravite de m et
pour celle tangente a la poulie, avec bien sur T' = T en modules. Le module T n'est pas egal a mg, puisque la masse m possede une acceleration.
Ceci fait, il n'y a plus qu'appliquer le PFD sur m et le theroreme du moment cinetique (TMC) sur la poulie :
a) sur m : +
= m.d2z/dt2.
, soit m.d2z/dt2 = mg - T' (eq. 1) ;
b) pour la poulie : 
=
, L etant le moment cinetique du disque par rapport a son axe de rotation passant par O, dont le module est L = J.d
/dt, avec J = (1/2)MR2 le moment d'inertie tjs par rapport a cet axe. Le moment de la force est TR ; on en tire TR = J.d2
/dt2 (eq.2).
Ton probleme est venu du fait que tu as cherche a appliquer le TMC a l'ensemble poulie + masse. Or la masse m ne tourne pas... sa vitesse et son acceleration sont lineaires, alors que pour la poulie elles sont angulaires.
Il manque encore une relation liant d2z/dt2 a d2/dt2, mais tu dois l'avoir trouvee donc je te la donne sans insister : c'est d2z/dt2 = R.d2/dt2.
En remplacant d2/dt2 en fonction de d2z/dt2 et en faisant T' = -T dans les relations precedentes, tu obtiendras deux equations dont les inconnues sont d2z/dt2 et la norme T de la tension.
Je te laisse faire les calculs et te donne simplement le resultat : d2z/dt2 = 2g/3 et T = mg/3. L'acceleration de la masse m n'est donc pas g mais elle est plus petyite, en raison de l'inertie de la poulie.
Si tu as d'autres questions a poser n'hesite pas, je suis quasiment en ligne jusque 23 heures. Prbebo.
petite rectification : dans mes relations vectorielles j'ai deja fait = -
: tu dois donc faire T' = T en modules, puisque le sgn - a deja ete pris en compte. Si tu as des soucis avec ca, ecris-moi. Prbebo.
Bonjour !
C'est tout à fait compris il s'agissait d'un problème de méthode de ma part.
J'ai vu différente façon de traiter ce problème par la suite.
Cependant dans votre résultat je ne comprends pas pourquoi vous trouvez d2z/dt2 = 2g/3
je trouve moi g/11 ( ce qui est correct car j'ai les solutions des valeurs que je dois trouver).
En tout cas merci énormement d'avoir pris le temps de me donner des explications aussi claires !
Marie.
Conservation de l'énergie macanique du système poulie + masse :
(1/2).m.v² + (1/2).J.w² = mgz
Avec J = MR²/2 et w=v/R (avec M la masse de la poulie)
(1/2).m.v² + (1/2).MR²/2 .v²/R² = mgz (avec z la distance parcourue par la masse m à l'instant t)
(1/2).m.v² + (1/4).M.v² = mgz
(1/2)*1.v² + (1/4)*20.v² = 1*gz
5,5*v² = gz
en dérivant par rapport au temps : 11.v.dv/dt = g.dz/dt
Or v = dz/dt ---> 11.dv/dt = g
dv/dt = g/11
a = g/11
C'est l'accélération de la masse.
w = v/R
dw/dt = (1/R).dv/dt
dw/dt = (a/R)
dw/dt = g/(11*0,5) = g/5,5
C'est l'accélération angulaire de la poulie (en rad/s si g est en m/s²)
-----
Sauf distraction.
A la fin de mon message précédent, lire :
C'est l'accélération angulaire de la poulie (en rad/s² si g est en m/s²)
Bonjour a tous les deux,
excusez-moi de reprendre ce topic tardivement, j'ai du m'occuper de pb familiaux plus urgents. Un grand merci a J-P d'avoir repondu a ma place et d'etre arrive a la solution (g/11), en suivant une autre demarche que la mienne.
dans mon premier post, tout est correct, il faut juste oublier la phrase d2z/dt2 = 2g/3 qui resulte d'une etourderie. Pour Miniminette, je reprends rapidement mes relations :
m.d2z/dt2 = mg - T (relation 1) ;
J.d2/dt2 =RT (relation 2) ;
d2/dt2 = d2z/dt2/R (relation 3) ;
J = (1/2).M.R2 (relation 4).
En remplacant dans (2) J et d2/dt2 donnes par (3) et (4), on obtient T = (1/2).M.d2z/dt2 ; avec (1), on arrive a m.d2z/dt2 = mg - (1/2).M.d2z/dt2, dont on tire d2z/dt2 = g.2m/(2m + M).
Avec m = 1 kg et M = 20 kg, ce coefficient 2m/(2m + M) vaut 1/11, ce qu'il fallait trouver.
Mon etourderie est que dans la derniere etape du calcul j'ai remplace M par m, ce qui donne 2g/3... oubliez ca tous les deux, jure ?
On a donc bien d2/dt2 = d2z/dt2/R = 9.8/5.5 rad.s-2, et egalement l'expression de la tension T du fil : T = (mg.M/(M + 2m) = mg.10/11.
Miniminette, ton pb est enfin resolu, et avec 2 methodes : le theoreme du moment cinetique associe au PFD, et le theoreme de l'energie cinetique.
A bientot, BB.
Annuler
connectez vous