Inscription / Connexion Nouveau Sujet
dynamique de rotation
bonjour,
Pour trouver la valeur de I0, il faut ici faire varier la masse m (m1 et m2) et les disques utilisés (rayons r1, r2 et r3) et mesurer les fonctions Teta=f(t) pour trouver les valeurs d'accélération angulaire Alpha correspondantes.
on sait que l'accélération angulaire 𝛼⃗ = 𝜔̇ ⃗𝑒⃗⃗⃗𝑧 et que la vitesse angulaire 𝜔⃗⃗ = 𝜃 ⃗𝑒⃗⃗⃗𝑧;
Déduire l'expression de Teta en fonction de t et de alpha. On prendra les vitesses et positions angulaires initiales égales à 0.
pour l'expression de Teta en fonction du temps c'est bien: d2 / dt2= Fsin Alpha ?
Bonjour
Tu utilises sans doute un pendule de torsion... Exact ?
Sinon, il faut décrire avec précision l'expérience réalisée et poser une question précise sur ce que tu ne comprends pas. Sinon : impossible de t'aider !
Comme déjà écrit : il faut décrire l'expérience réalisée, copier les questions qui sont posées et expliquer ce que tu ne comprends pas !
l'experience est sur le sujet:
Du point de vue de la Dynamique, la masse est la propriété d'un objet qui s'oppose à la variation de son état de mouvement (sa vitesse). Dans la Dynamique de la rotation, le moment d'inertie possède un rôle équivalent : c'est la propriété d'un objet qui s'oppose à la variation de sa vitesse de rotation
̇ 𝜔 = 𝜃.
Cette première expérience a pour objectif de vous faire déterminer la valeur du moment d'inertie I0 du système d'étude sans masse ajoutée. Pour cela vous utiliserez l'équation :
∑ 𝑀0 = 𝐼 𝛼⃗
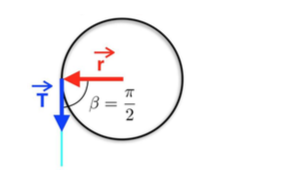
Si l'on néglige les forces de frottement, le seul moment à prendre en compte correspond à celui de la force de tension 𝑇 du fil :
𝑀 = 𝑟⃗ ∧ 𝑇 = 𝑟𝑇𝑠𝑖𝑛𝛽 = 𝑟𝑇 car ß=π/2
La force de tension du fil est égale au poids de la masse accroché au bout du fil (mg). Comme résul- tat on obtient dans le cas du système sans masse ajoutée :
r m g = Io Alpha
image:
Pour trouver la valeur de I0, il faut ici faire varier la masse m (m1 et m2) et les disques utilisés (rayons r1, r2 et r3) et mesurer les fonctions Teta=f(t) pour trouver les valeurs d'accélération angulaire Alpha correspondantes.
La force de tension du fil est égale au poids de la masse accroché au bout du fil (mg)
J'espère que cette phrase n'est pas de ton professeur car elle est totalement fausse et catastrophique sur le plan pédagogique !
Le théorème des moments que tu as écrit conduit bien à :
r.T=Io.
 en notant
en notant  l'accélération angulaire. En revanche, poser T=m.g est totalement faux. Il suffit d'appliquer la relation fondamentale de la dynamique à la masse m en mouvement rectiligne vertical :
l'accélération angulaire. En revanche, poser T=m.g est totalement faux. Il suffit d'appliquer la relation fondamentale de la dynamique à la masse m en mouvement rectiligne vertical :
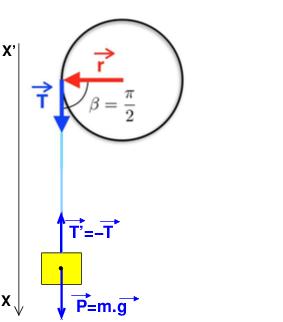
En projetant sur l'axe (X'X) et en passant aux normes de vecteur, sachant que la norme de la tension est la même tout au long de la corde :
-T+m.g=m.a soit : T=m(g-a) et non T=m.g comme tu l'as écrit. Je te laisse rectifier. Il faut juste remarquer que l'accélération a de la masse est égale à :
a=r.

Il est possible, au niveau des mesures que cela ne change pas grand chose si le dispositif est tel que Io>>m.r2 ; de là à enseigner délibérément quelque chose de faux ...
Je te suggère donc de faire la démonstration rigoureuse, quitte à faire ensuite des approximations si elles sont justifiées...
du coup pour la réponse à: Déduire l'expression de Teta en fonction de t (temps) et de alpha dont on prendra les vitesses et positions angulaires initiales égales à 0.
c'est bien: d2 Teta / dt2= F*sin Alpha
ou Teta =1/2 alpha (tf - ti)2 + w (tf-ti)
je m'excuse de ne pas réussir, j'ai vraiment du mal avec la mécanique
Le théorème du moment dynamique appliqué à un solide en rotation autour d'un axe fixe s'écrit :
car :
La relation fondamentale de la dynamique appliquée à la masse m en translation verticale s'écrit :
soit en projetant sur l'axe (X'X) :
T=m(g-a)
Le fil ne glisse pas sur la roue : a=r .
.
En reportant au-dessus :
Je te laisse simplifier :
A vérifier : si mr2<<Io : l'expression peut se simplifier pour donner celle de ton professeur :
Pour juger, il faudrait avoir les caractéristiques du dispositif...
a étant une constante, par intégration la vitesse angulaire a pour expression :
avec
 o : vitesse angulaire à l'instant initial (valeur peut-être nulle ?)
o : vitesse angulaire à l'instant initial (valeur peut-être nulle ?)
En intégrant une seconde fois :
avec
 o : valeur initiale de
o : valeur initiale de  : sans doute valeur choisie nulle.
: sans doute valeur choisie nulle.
Il faudrait connaître les mesures réalisées pour en dire plus...
merci, j'ai réussi à répondre a cette question.
est ce que je peux poser une autre question sur ce meme devoir ou je doit refaire un sujet ?
je dois vérifier la formule 𝐈 = ∑𝐢 m𝐢 ∧ 𝐫𝐢𝟐
"Pour cela vous allez fixer la valeur du moment de la force de tension du fil appliquée, MT,o = r2 m1g et faire varier la distribution des masses sur la barre du système d'étude. L'équation s'écrit:
r2 .m1 . g=Itot .Alpha
où Itot = I0 + ∑i mi ∧ Ri2
1- Réalises des mesures expérimentales de Teta= f(t) pour 3 valeurs différentes de masses de chaque côté de la barre (mc, 2mc et 3mc) et 3 valeurs de R : 5 cm, 12 cm et 20 cm.
2- ensuite, trouves les variables pour les axes des graphiques (en fonction de alpha et du temps t) de façon à obtenir une droite de pente proportionnelle à la valeur de l'accélération angulaire alpha.
3- Représenter sur un même graphique les courbes obtenues pour chacune des 9 expériences
4- en Déduire les valeurs de l'accélération angulaire pour chacune des 9 expériences.
5- Calculer les valeurs de Itot en fonction de g,Alpha r2 et m1 pour chacune des 9 expériences.
6- Représentes graphiquement les valeurs de I tot en fonction de ∑i mi ∧ Ri2
je bloque pour la 4eme et la 5eme question


