Inscription / Connexion Nouveau Sujet
Domaine de fréquence
Re,
J'ai deux montages en électronique avec deux fonctions de transfert que j'ai établi :
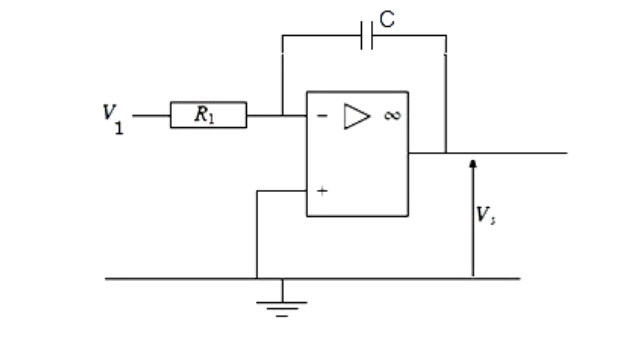
(montage 1 intégrateur)
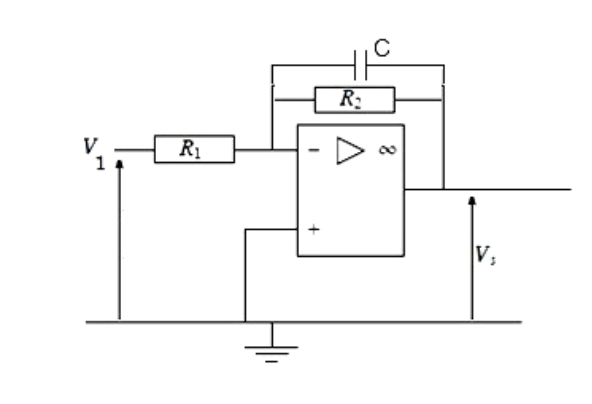
(montage 2)
Je dois trouver le domaine de fréquence tel que le montage 2 fonctionne comme un intégrateur (montage 1), mais je ne sais pas comment procéder.
Il y a plusieurs façons possibles d'arriver à la réponse.
1° : la plus "physique" à mon avis : Suppose R2>>Zc soit R2C >>1: le courant traversant R1 passera de façon quasi intégrale dans la branche du condensateur (loi sur les diviseurs de courant) ; le montage 2, vis à vis d'un signal alternatif, sera donc équivalent au circuit 1. Alors qu'au contraire, si Zc>>R2, tout va se passer comme si le condensateur n'existait pas : le montage sera équivalent à un ampli inverseur (ou atténuateur inverseur si R2<R1).
>>1: le courant traversant R1 passera de façon quasi intégrale dans la branche du condensateur (loi sur les diviseurs de courant) ; le montage 2, vis à vis d'un signal alternatif, sera donc équivalent au circuit 1. Alors qu'au contraire, si Zc>>R2, tout va se passer comme si le condensateur n'existait pas : le montage sera équivalent à un ampli inverseur (ou atténuateur inverseur si R2<R1).
2° : la plus "mathématique" et la plus directe :
R2C >>1 : H2
>>1 : H2 H1 : le circuit se comporte en intégrateur inverseur ;
H1 : le circuit se comporte en intégrateur inverseur ;
R2C <<1 : H2
<<1 : H2 -(R2/R1) : le circuit se comporte en ampli inverseur (ou éventuellement atténuateur inverseur si R2<R1)
-(R2/R1) : le circuit se comporte en ampli inverseur (ou éventuellement atténuateur inverseur si R2<R1)
Remarque n° 1 : avec les ampli op réels le montage n° 1 ne fonctionne pas correctement : un courant continu de défaut produit par l'ampli op charge le condenseur et fait dériver la tension de sortie vers +Vsat ou -Vsat selon le sens de ce courant de défaut. Si on désire intégrer un signal périodique, on choisit toujours le montage n° 2 en choisissant R2C grand devant 1. Tu verras sans doute cela en travaux pratiques...
grand devant 1. Tu verras sans doute cela en travaux pratiques...
Remarque n° 2 : la condition R2C peut être un peu mieux précisée. Il suffit en fait , pour obtenir un comportement d'intégrateur pour le montage n° 2 avec une précision acceptable, que son diagramme de Bode du gain soit assimilable à son asymptote oblique. Ceci est en bonne approximation le cas dès que R2C
peut être un peu mieux précisée. Il suffit en fait , pour obtenir un comportement d'intégrateur pour le montage n° 2 avec une précision acceptable, que son diagramme de Bode du gain soit assimilable à son asymptote oblique. Ceci est en bonne approximation le cas dès que R2C >
> 10...
10...
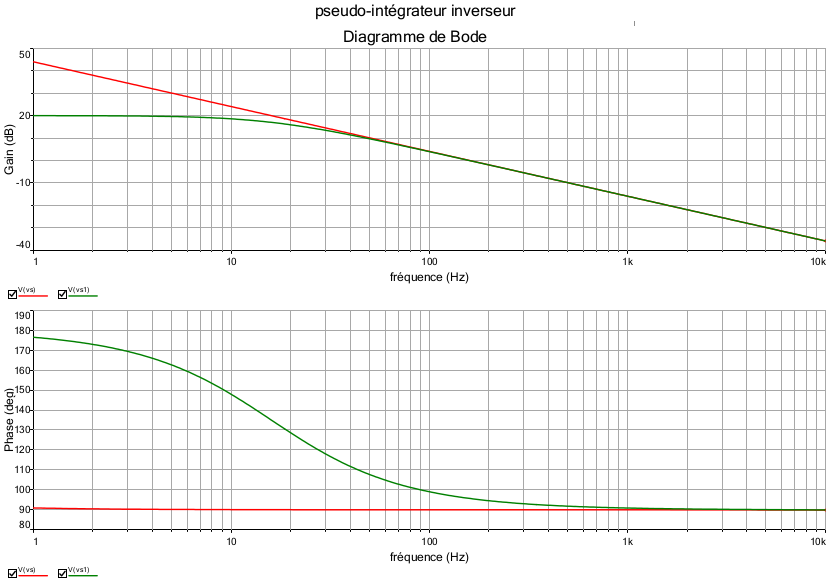
Je ne sais pas si tu as étudié déjà les diagrammes de Bode. Si oui, les diagrammes comparés correspondant au montage 1 (en rouge) et au montage 2 (en vert) pourront t'aider.
Pour l'intégrateur inverseur (montage 1), le diagramme du gain correspond à une droite de pente -20dB/décade alors que la phase est constante : 90°
Pour le montage 2 : on distingue nettement deux domaines de fréquences où le fonctionnement est simple :
basses fréquence : comportement d'ampli inverseur avec G2=20.log(R2/R1)=20dB et une phase voisine de 180°
haute fréquence : comportement d'intégrateur inverseur : le diagramme du gain et celui de la phase ce confondent avec ceux du montage n° 1.
Pour le tracé, j'ai choisi arbitrairement :
R1.C=10-3s ; R2=10R1
Oui, j'ai déjà un peu étudié les diagrammes de Bode dans le cas des filtres (circuits RLC).
C'est prévu qu'on les étudie pour les AOP, merci pour les exemples donnés avec ces graphiques ! 
J'ai une question concernant la phase, c'est bien avec ceci que l'on constate que l'AOP du montage 1 est inverseur pour les basses fréquences puisque le décalage de phase est de 180° ?
Tu as raison :
de façon générale en régime sinusoïdal, pour le second montage :
Cas limites simples :
Si :
alors :
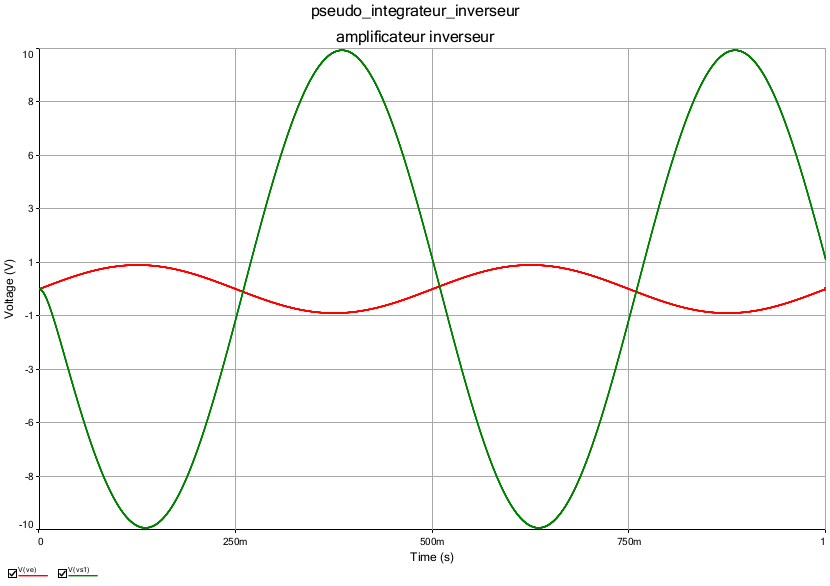
Avec R2=10.R1, le montage est bien amplificateur et inverseur : l'amplitude est multipliée par 10 et la tension de sortie est en opposition de phase par rapport à la tension d'entrée.
La primitive sinusoïdale de ve(t) s'écrit :
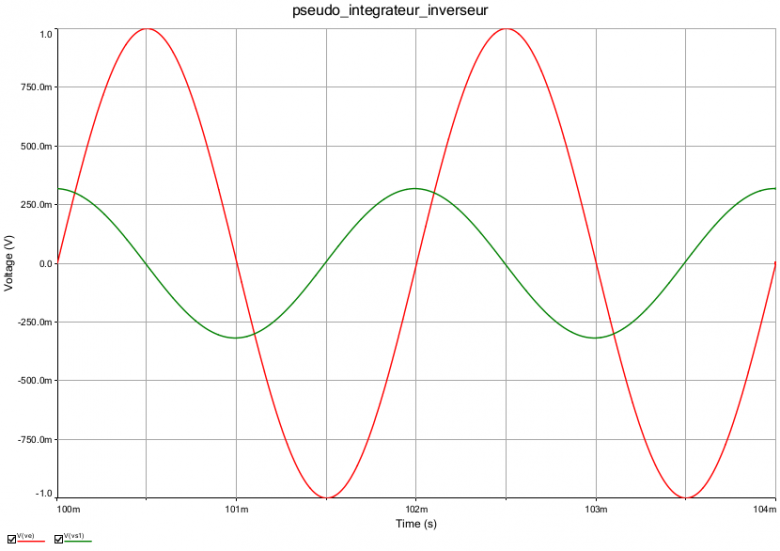
On voit bien que la tension de sortie est proportionnelle à l'opposée de la primitive sinusoïdale de la tension d'entrée. Le montage peut donc être qualifié d'intégrateur inverseur.
Si tu as un peu de temps, tu peux vérifier cela sur les deux simulation ci-dessous. Les caractéristiques du circuits sont celles définies dans mon message précédent. La première simulation correspond à f = 2Hz, la seconde à f=500Hz ; Vem=1V