Bonsoir,
Une méthode possible consiste à montrer que le vecteur dérivée de R par rapport au temps est le vecteur nul à chaque instant. Si on dérive  :


En remplaçant le vecteur accélération par son expression générale et le vecteur moment cinétique en O par son expression générale, on y arrive !

Précision : contrairement à ce que tu as écrit, le vecteur u_r est de norme fixe mais sa direction et son sens varient au cours du mouvement.
Le vecteur vitesse est de direction et de sens  variables au cours du mouvement. De plus, il n'est pas nécessaire de supposer que sa norme est fixe pour aboutir au résultat demandé.

Qu'est ce qui permet, dans l'énoncé, de supposer que l'orbite est circulaire ?

Beaucoup de satellites ont une orbites quasi circulaires ... mais beaucoup d'autres non.
Tout dépend du but recherché.
Un exemple (parmi plein d'autres) sont les satellites avec une orbite de Molnia.

Rien ne dit dans l'énoncé que l'orbite est circulaire. Il n'est pas nécessaire de faire cette hypothèse pour démontrer que le vecteur R est constant.

Merci Vannoise.

Cependant en appliquant cette méthode, je ne fait que bloquer.
J'ai remplacer l'accélération et le moment cinétique. Et en polaire je remarque que rien ne s'annule spontanément.
Je passe en coordonnée cartésienne, espérant que cela se simplifie. Mais si simplification, il y a. C'est vraiment pas évident.

L'expression sur laquelle je tombe  est :


Je m'attend en passant en cartésien à ce que les composants en x et y s'annule.

Accélération :



Moment cinétique calculé au point O :



Je te laisse terminer...

Oui, oui, là il est bien sûr évident que vaut 0 . Merci, ce que j'avais fait avais été de passer par la définition du vecteur position en polaire et dérivée 2 fois pour trouver l'accélération. C'était devenue une expression monstrueuse...

5)Déterminez l'expression de sous la forme :


J'ai trouvée que :



6)En calculant de 2 façon différentes le produit scalaire, montrer que .

Pour , les résulats de la 5) marche parfaitement car des simplifications trigonométriques interviennent et multipliant coordonnées à coordonnées.

Ma gène vient à . Sachant que , le produit scalaire idéale serait celui ou
. Et ce serait gagné.

Je n'ai pas d'idée vue comment les expressions se complexifie rapidement.

Juste une petite correction à ce que je raconte :

est bien sûr la constante des aires.

Tu as bien travaillé ! Puisque tu as démontré que le vecteur R est un vecteur constant. Tu peux déterminer ce vecteur dans les conditions particulières de l'instant initial. Je te laisse faire le calcul : tu vas facilement obtenir :



où R_o est une constante qui est aussi égale au R_x qui te gêne ! Le « but du jeux » est d'obtenir, assez simplement l'équation polaire de la trajectoire sous la forme classique :



où e désigne l'excentricité et p le paramètre de la conique.

Tout à fait, d'après les conditions initiales :


Ainsi on trouve que :



D'où le calcul scalaire est aisément obtenus.

7) Déduire .

On a obtenu la relation
En isolant r et factorisant pour obtenir la forme demandée, je trouve :


Par identification :


8)Déterminez les valeurs de permettant d'obtenir un cercle(e=0), une ellipse(0<e<1), une parabole(e=1) et une hyperbole(e>1).

On me donne ici, des conditions sur e.
Je les applique alors. Mais ma réponse pour la parabole me gène,



Mon professeur de physique, nous avait expliqué que la parabole était un cas purement hypotéthique dans la réalité. Où l'objet partait d'une vitesse initiale nulle. Mais attirée par l'attraction gravitaionnelle en accumulerait. Elle correspond à la séparatrice sur le digramme énergie potentielle.

Je ne sais pas si ce que j'ai trouvée là, semble cohérent. Est-ce que mon e et p sont bon ?
Sans quoi tout est faux, forcément.

D'accord avec tes résultats pour 7)
Pour 8 : il ne faut pas oublier que la constante des aires dépend de v_o. Tu as tout intérêt à remplacer C par r_o.v_o² avec r_o=Rt+h_o.
Le cas particulier e=1 est effectivement un cas limite qui correspond à une énergie mécanique nulle. Ce cas est effectivement quasi impossible à obtenir pratiquement car il faudrait être capable de régler exactement la valeur de v_o à :


On voit bien dans ce cas que l'énergie mécanique est nulle avec les conventions habituelles pour l'état d'énergie potentielle nulle :


C'est l'énergie mécanique qui est nulle, pas la vitesse initiale...

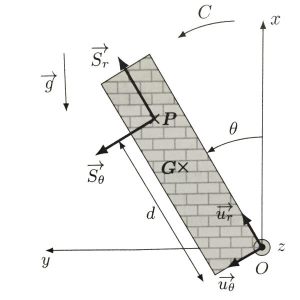
Voilà un nouveau problème sur cette fois la chute d'une cheminée.

Une cheminée verticale est modélisée par un cylindre de masse M et homogène.
Cette dernière va chuter. On appelle , l'angle de la cheminée avec la verticale.

1) Déterminez, grâce au TMC en projection sur Oz, l'équation du mvt vérifiée par l'angle .

Alors, ici considérant le solide entier. Je l'applique à un point quelconque M le long de la cheminée .
Bilan des forces:
-poids appliquée en M  
-réaction en O

Alors en partant de :
(1)
j'arrive à
(2)  
Avec

2)Exprimer l'énergie mécanique de la cheminée. Mq elle se conserve et retrouver l'équation du mouvement de la cheminée.

Je suis repartie de de la 1) et ait multipliée par pour faire apparaître les dérivées de l'énergie cinétique et potentiel:




On reconnait l'énergie cinétique, et l'énergie potentielle.



Donc Em=cste.

Par contre, je voit pas de quoi, on parle quand on demande l'équation du mouvement de la cheminée. J'ai déjà établis une équation du mouvement. Quelle différence, ici ?

Petite remarque préliminaire : pour la bonne lisibilité du forum, il aurait été préférable de créer un nouveau topic puisqu'il s'agit d'un problème indépendant du précédent.
Sinon, d'accord avec ton raisonnement mais il me semble que tu as commis une erreur de signe. Tu aurais pu t'en apercevoir en testant le réalisme de tes formules : en basculant, la cheminée subit une accélération angulaire pas un freinage. De même, en choisissant le niveau d'énergie potentielle nul en x=0, cette énergie potentielle est positive pour compris entre zéro et /2 rad.
De plus, ce raisonnement me semble plus compliqué que celui effectivement demandé ici : tous les étudiants ne connaissent pas la technique du "facteur intégrant" !
A mon avis, la question 2 demande simplement de poser l'expression de l'énergie potentielle telle qu'elle a été démontrée en cours . La conservation de cette énergie mécanique (frottements négligés) impose :


Il suffit alors de vérifier que la dérivation par rapport au temps de l'expression de l'énergie mécanique conduit à l'équation différentielle obtenue en 1).
Par équation du mouvement, il faut je pense comprendre : établir l'équation différentielle vérifiée par . Il n'existe d'ailleurs pas de solution explicite à cette équation différentielle...

Je suis passé un peu vite sur ta solution. Je n'ai pas l'énoncé intégral mais à priori rien n'indique que la hauteur H de la cheminée soit très grande devant son rayon Rc.

De plus, le théorème du moment cinétique est appliqué au solide, pas à un point M quelconque. Nous sommes maintenant en mécanique du solide. J_o doit désigner le moment d'inertie du solide par rapport à l'axe (O,z) et le moment du poids se calcule comme si le poids était une force appliquée en G. Dans ces conditions, le théorème du moment cinétique appliqué en O au cylindre s'écrit :



La résultante de l'action de l'axe sur le cylindre n'est pas dans le cas général colinéaire au vecteur mais le moment de cette action par rapport à l'axe de rotation est nul.
Sous toutes réserves ; je n'ai pas l'énoncé intégral...

Bonjour,

En fait il est dit dans l'énoncée que la cheminée est  de longueur D et de rayon très petit devant D. Cependant, je pense que la mécanique du solide est toujours valable ici.

Par contre, cela voudrait simplement dire que l'on a . Ce qui me simplifierait grandement mon produit vectoriel.

Par ailleurs, oui comme équation du mouvement on obtient :

Où :


Ce qui là semble être cohérent par rapport à l'énergie potentiel.

Bien sûr le omega zero est au carrée.

Alors l'expression complète de l'éqn du mouvement est :

(1)

Parce que en intégrant je retrouve l'équation de l'énergie mécanique je sais que :


Donc je refait le chemin inverse pour répondre correctement à la question :
par définition et C=0.

Ou projetée de G sur l'axe x, chose logique car l'énergie potentiel ne dépend ici que de la hauteur en x.

Par remplacement de formules :


Alors que ce que je voudrait serait en , mais c'est à cause de la formule de je bloque.

Je n'arrive pas à trouver l'erreur pour corriger ce fait.

Je reprends le calcul du moment du poids intervenant dans le théorème du moment cinétique ;



Puisque :




D'où l'équation différentielle :


Il me semble avoir abordé cela avec toi. Pour chaque « formule » démontrée, il faut vérifier l'homogénéité mais aussi le réalisme. Il est facile ici de remarquer que le moment du poids est nul pour =0 et maximum pour . Cette remarque permet de détecter une éventuelle confusion entre sinus et cosinus.
Tu devrais t'en sortir maintenant...