Inscription / Connexion Nouveau Sujet
dm de mécaniqe
Bonjour, je suis bloqué à cet exercice de mécanique pourriez-vous m'aider?
énoncé:
Une échelle double se compose de deux échelles simples AO et BO de même longueur L, de centres d'inertie G1 et G2 (respectivement), de même masse m, articulées sans frottement au sommet commun O (liaison pivot parfaite d'axe Oz).
On note 2alpha l'angle au sommet des deux échelles. Ces deux échelles sont en appui sur le sol en A et B. On note f le coefficient de frottement entre les échelles et le sol.
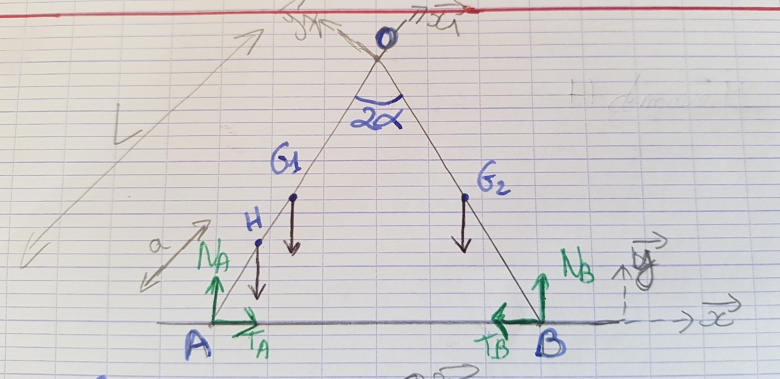
Une personne de masse M monte l'échelle AO. Elle se situe au point H de la figure ci-dessous (sachant que la longueur AH est notée a).
1) Déterminer les efforts exercés en A, B et O lorsque l'échelle est en équilibre en fonction de m, M, a, L et alpha .
2) Exprimer la condition d'adhérence en A et B.
3) En déduire lequel des deux points de contact est susceptible de glisser en premier si on fait varier l'angle alpha.
4) Dans le cas où la masse de l'échelle est négligeable devant la masse de l'utilisateur (M ≫ m), quel est l'angle maximal d'ouverture de l'échelle (α) pour que la personne puisse monter jusqu'en haut sans risque ?
mes recherches:
j'ai terminé le BAME de la question 1 mais j'ai un soucis pour mettre tous les moments au point O, ce soucis c'est comment faire la figure de calcul avec l'angle alpha
pourriez vous m'aider à continuer?
Bonsoir
Si tu pouvais scanner et poster ici le schéma avec les différents vecteurs force, il serait plus facile de t'aider efficacement ensuite.
Excellent schéma !
Tu peux d'abord choisir comme système l'échelle double et lui appliquer les lois de la statique. La résultante des vecteur forces est le vecteur nul.
La projection sur un axe horizontal de cette relation te donne une relation simple entre TA et TB
La projection sur un axe vertical te donne simplement la somme NA+NB.
Le fait que l'échelle ne tourne pas autour d'un axe perpendiculaire au plan de figure passant par A te donne simplement NB par application du théorème des moments statiques. Tu en déduis ensuite simplement NA.
Pour la suite, il faut appliquer les lois de la statique à l'échelle OB ou à l'échelle OA.
Jusqu'à maintenant jessai de isoler OA puis OB apres avoir fait le BAME mais au moments de calculer les moments je bloque sur comment faire les figures de calculer et plus précisément placé langle dessus
Non,car je nai pas vraiment compris
Désolé
Ce que jessayais de faire cest ce que notre prof nous a dit de faire poir resoudre le problème
Je ne sais pas ce que tu appelles le BAME !
Dans un premier temps, écris que la somme vectorielles de toutes les actions extérieures à l'échelle double est le vecteur nul et projette sur un axe horizontal puis sur un axe horizontal.
ce que j'appelle le BAME c'est le bilan des actions mecaniques extérieurs
c'est à dire appliqué à OA:
il y a 4 actions:
-gravité sur échelle
-gravité sur l'homme
-sol sur échelle
-liaison pivot en O
et pour ces 4 actions j'ai écrit les torseurs correspondant
je ne vois pas comment écrire la somme vectorielle sur l'échelle double
Non ! Et c'est toute l'astuce de la méthode : si tu choisis comme système l'échelle double : les actions en O sont considérées comme des actions intérieures et n'ont pas à être prises en compte.
Pour étudier les actions en O, il faut étudier une échelle seule comme je l'ai expliqué dans mon premier message.
ce que j'ai écris la concerne une échelle seule OA
pour l'échelle double du coup ce serai donc je pense:
-gravité sur échelle(*2)
-gravité sur l'homme
-sol sur échelle(*2)
Non plus !
Si tu choisis comme système la seule échelle OA, il faut, aux forces que tu cites, ajouter l'action de l'échelle OB.
Pourquoi ne veux-tu pas suivre l'ordre logique que je t'ai indiqué dans mon premier message ?
ce n'est pas que je ne veux pas le suivre au contraire je ne comprends tout simplement pas comment le faire
Juste pour te mettre sur la voie ; je choisis, dans un premier temps, comme système, l'échelle double. Les actions extérieures appliquées sont :
Les poids des échelles
l'action de l'homme égale à son poids
les actions du sol en A et en B.
Principe fondamental de la statique :
projection sur un axe horizontal :
Projection sur un axe vertical :
La somme des moments en A de ces forces est nulle. Je te laisse faire le calcul. Tu vas obtenir NB. Puisque tu as entendu parler de torseur, tu sais sûrement calculer les différents moments...
Je trouve tout de même cet exercice un peu difficile pour ton niveau...
D'accord
La tu me dis que la somme des moments en A est nulle mais vu que le système cest toute lechelle cest le cas aussi en les autres points non?
Pour le calcul du moment en A normalement je sais le faire mais jai un probleme je narrive pas a faire la figure de calcul qui vas avec cest a dire placé langle alpha sur la figure de facon a trouver les angles correct quand je fais le produit vectoriel
Il est exact qu'en statistique, la somme des moments des actions extérieures est nulle en tout point. C'est en choisissant le point A qu'il est facile d'obtenir l'expression de NB.
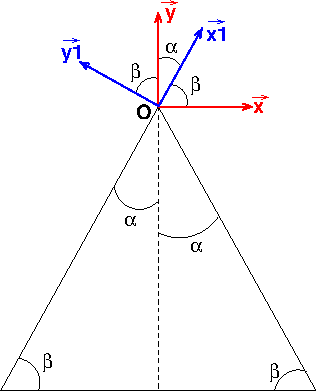
La verticale passant par O est la bissectrice de l'angle 2 en O. Tu retrouves donc l'angle
en O. Tu retrouves donc l'angle  entre x1 et y.
entre x1 et y.
J'explique ma pensée avec ce schéma :
Desole si je pose autant de questions , je veux juste sortir de ce dm en ayant compris car a la rentrée j'ai un ds de mécanique qui risque de ressembler a ca sur le principe
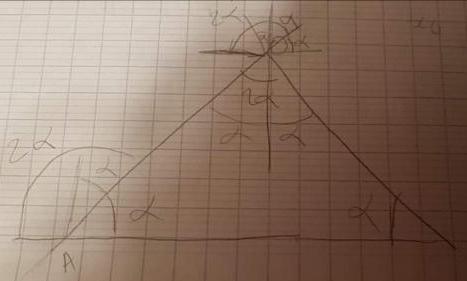
je suis tout a fait d'accord avec le schéma du coup pour les calculs je dois prendre l'angle alpha non?
L'énoncé fournit l'angle  . Les résultats doivent faire intervenir
. Les résultats doivent faire intervenir  . Tu peux utiliser
. Tu peux utiliser  comme intermédiaire de calcul. Comme ces deux angles sont complémentaires, le sinus de l'un est égal au cosinus de l'autre.
comme intermédiaire de calcul. Comme ces deux angles sont complémentaires, le sinus de l'un est égal au cosinus de l'autre.
Quelqu'un qui a eu un cours sur la notion de torseur sait nécessairement calculer le moment d'une force...
du coup je calcul les moments en A des différentes actions avec la relation de Varignon et je dis que la somme de ces moments est nuls et donc j'ai une équation selon z dans laquelle je dois isoler Nb c'est bien ça?
une fois que j'aurais calculé exprimer ca je dois en déduire Na ou je peux pas encore ?
ensuite, je dois isoler une seule échelle?
Le calcul du moment donne NB. La relation fondamentale de la dynamique t'as fourni précédemment la somme NA+NB...
Que vient faire la formule de Varignon dans un problème de statique ? Il s'agit ici de moments de forces par rapport à un point ou par rapport à un axe....
Je refuse de te fournir directement une solution car il existe plusieurs façons de calculer ces moments de forces et sans connaître la méthode de ton cours, je risque de t'embrouiller...
pour les moments en A:
pour l'homme(H): -Mgcos

pour la gravité sur OA:-mgL/2*cos

pour la gravité sur OB: (Lmg*cos -Lmg/2sin
-Lmg/2sin )
)
pour l'action du sol sur le coté OB: (LTbsin +LNbsin
+LNbsin )
)
pour l'action du sol sur OA c'est 0
ensuite, la somme de tous ça=0
donc: -Mgcos -mgL/2*cos
-mgL/2*cos +Lmg*cos
+Lmg*cos -Lmg/2sin
-Lmg/2sin +LTbsin
+LTbsin +LNbsin
+LNbsin =0
=0
Quelques erreurs : la distance a = AH doit intervenir pour le moment du poids de l'homme.
Le moment de TB en A est nul (revoir le cours). La distance AB vaut 2L.sin( )
)
désole pour l'homme j'ai fait une faute de transcriptions j'ai -Mga cos 
pourquoi Tb serais nul je veux dire le moment est nul en son points d'application qui est pour moi B
oui la distance AB fait 2Lsin alpha je bloque sur le calcul je pense je vais essayer de voir mes erreurs
Selon moi :
Je te laisse simplifier et vérifier. Il pourrait être intéressant de faire apparaître le rapport ...
La ligne d'action de la force TB passe par le point A. Son moment en A est donc nul. Revois ton cours sur la notion de moment.
Ok tres bien
Je regarderai et continuerai demain matin
Pk tu as des sin partout alors que jai quasiment que des cos
Cest pas -cos = sin?
je viens de regarder j'ai réussi à retrouver quasiment tous les éléments sauf 1 qui est mg 2Lsin alpha
J'ai juste écrit que le "bras de levier" du poids de l'échelle OB est égal à la distance de A à la verticale passant par G2. Cette distance est la différence entre la distance AB et la distance de B à la verticale passant par G2.
Remarque : la somme des moments des deux poids des deux échelles peut aussi s'obtenir en considérant que le poids total de l'échelle double est 2mg et que le centre de gravité G de l'échelle double est le milieu du segment G1G2.
ensuite j'ai isolé OA :
j'obtiens selon x: Ta + X21=0
selon y: -mg-Mg+Na+Y21=0
et pour les moments je les ai mis au point O :
-Lmg/2sin  +Mg(L-a)sin
+Mg(L-a)sin  +LTasin
+LTasin +LNasin
+LNasin 
D'accord avec ton expression de NB. Ensuite : étourderie de copie ou erreur de signe : je ne sais pas. La somme NA+NB a une expression simple qui n'est pas vérifiée avec ton expression de NA.
Ensuite : tu as isolé OA : pourquoi pas mais il est plus simple d'isoler OB car il y a une force en moins à prendre en compte.
Attention : le moment de TB comme celui de TA fait intervenir L.cos( ).
).
je viens de regrader a nouveau mes calculs et en effet j'ai fait une erreur de signe
j'obtiens Na=g(M+m-Ma/2L)
j'ai isolé OB:
selon x: -Tb-X21=0
selon y: Nb-Y21=0
pour les moments en 0 :
-mgL/2sin +TbLsin
+TbLsin +NbLsin
+NbLsin =0
=0
pour le moment en O:
je pense avoir fait une erreur:
je viens de le refaire j'obtiens maintenant: LNbsin
après une longue réfléxion j'ai trouvé Tb=g(-Ma/2L-m+m/2) et donc Ta est égale à la même chose
Y21=Nb trouvé précédemment
et -X21=Tb
la je crois que la question 1 est terminé non?
pour la 2 c'est la loi de coulomb:
condition d'adhérence: norme vecteur tangentielle f * norme vecteur normale
f * norme vecteur normale
pour la 3 par contre je ne vois pas comment y répondre
Effectivement :
On isole maintenant l'échelle OB :
Théorème des moments statiques en O :
En remplaçant NB par la valeur ci-dessus, on obtient :
En supposant la liaison pivot en O parfaite, l'action de l'échelle OA sur l'échelle OB est équivalente à une force F de vecteur :
Équilibre de l'échelle OB :
Principe des actions réciproque (appelé aussi principe de l'action et de la réaction) : l'action de l'échelle OB sur l'échelle OA est équivalente à une force F' telle que :
Je te laisse continuer ; la suite est plus facile.
Pour 3 : puisque TA=TB et que NA>NB il est assez facile de prévoir laquelle des deux échelles va commencer la première à glisser en premier pour 0<a<L.
pour l'équilibre OA: -1/2g tan
pour la question 3 c'est donc le point de contact B qui glissera en premier
pour la question 4 je vois pas trop
ok je vais regarder pour la question 4
j'ai 2 petites questions pour avoir parfaitement compris la question1:
la premiere: pourquoi on transforme des cos en sin puis apres on laisse le cos
la deuxième: enfaite quel était le but précis de la question je veux dire les effort exercés ça veut dire quoi par rapport à tous ce que on a calculé?
L'action d'un corps sur un autre est aussi appelée, surtout en sciences industrielles, effort et est décrite par un torseur. Lorsque ce torseur est un glisseur (pas un couple), on peut utiliser le mot force à la place d'effort ou d'action.
Le but final de ce problème est de pouvoir répondre à la question 4. Pour cela, il faut nécessairement avoir avant déterminé les actions normales et tangentielles du sol en A et en B. Le calcul des actions en O n'est pas utile au reste du problème. Peut-être s'agit-il juste de tester les connaissances sur le principe des actions réciproques ?
Peut-être te serait-il utile de bien revoir les définitions des fonctions trigonométriques et leurs applications au triangle rectangle.