Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

disque chargé tournant

Posté par
ferality 10-03-21 à 00:24

Bonjour à tous,

J'ai un exercice de niveau L2 physique à faire mais je rencontre des difficultés.
L'énoncé est le suivant :

On a un disque plan de rayon R, avec une densité de charge surfacique σ.
On fait tourner ce disque avec une vitesse angulaire ω.

Questions :
1. On considère dans un premier temps une spire de rayon r, parcourue par un courant I. Calculer le champ magnétique créé en un point M de l'axe Oz de la spire.

J'ai calculé en appliquant la loi de Biot et Savard pour un élément infinitésimal de spire sur un point M de l'axe (Oz), puis en intégrant sur \theta entre 0 et 2\pi.

Je trouve : \vec{B(M)}=\dfrac{\mu_0 I R^2 \vec{u_z}}{2(R^2+z^2)^{3/2}}. Je pense que c'est bon mais peut-être y a-t-il plus simple à faire avec le théorème d'Ampère ?

2. Le disque qui tourne est parcouru par une densité surfacique de courant jS. Exprimer la charge élémentaire couvrant la surface dS = rdθdr. En déduire le courant dI qui circule dans la « spire » de rayon r et de largeur dr et la densité surfacique de courant en fonction de la distance au centre.

Ici je ne suis pas bien sûr, j'ai fait ça : dq=\sigma dS = \sigma rd\theta dr
Donc on a \dfrac{dq}{dt} = \dfrac{\sigma r d\theta dr}{dt} = \sigma r\omega\dfrac{dr}{dt}
r ne varie pas ici donc \dfrac{dr}{dt}=dr ?
De plus d'après le cours, dI = \dfrac{d^2q}{dt}, donc il faudrait encore dériver... et on se retrouverait avec l'accélération angulaire or ça n'a pas de sens... je ne comprend pas.

3. Montrer que le courant total qui circule dans le disque vaut I = \sigma\omega\dfrac{R^2}{2}

4. En utilisant le résultat des deux premières questions, calculer le champ magnétique créé en M (sur l'axe Oz) par le disque en rotation.

5. Que devient ce résultat si on change le sens de rotation du disque ?

6. On suppose maintenant que le point M est très éloigné du disque. Donnez l'expression du champ en M en faisant un développement limité à l'ordre 4 en z du résultat obtenu à la question 4.

7. A grande distance, le disque peut être considéré comme un dipôle magnétique. Calculer son moment \vec{M}.

8. On rappelle que le champ créé à grande distance par un dipôle magnétique au point M situé dans la direction  \vec{e_r} et à la distance r, s'écrit :

\vec{B} = \dfrac{\mu_0}{4\pi}\dfrac{(3\vec{M}\cdot\vec{e_r})\vec{e_r}-\vec{M}}{r^3}

Appliquer  ce  résultat  pour  calculer  le  champ  magnétique  créé  au  point  M  et  comparer  au résultat obtenu à la question 6.

On rappelle :  (1+x)^a = 1+ax+\dfrac{a(a-1)}{2}x^2 + O(x^3)


Merci d'avance pour votre aide !

Posté par
gts2re : disque chargé tournant 10-03-21 à 07:06

Bonjour,

Pour le 1), on ne peut utiliser le théorème d'Ampère : pas assez de symétrie pour trouver un parcours utile. Le résultat est correct.

Pour le 2, votre dq est en fait un d2q, vous avez une surface (deux dimensions, certains d'ailleurs notent cela d2S) et deux variables r et .  \dfrac{d^2q}{dt} = \dfrac{\sigma r d\theta dr}{dt} donne \sigma r\omega dr car \omega=\frac{d\theta}{dt}. Ceci étant cela marche par homogénéité, mais il faudra rédiger pour montrer que votre \dfrac{d^2q}{dt}   est bien un courant, c'est-à-dire une charge traversant une surface (en fait ici une ligne) par unité de temps.

Pour le 3, cela sera une simple intégration

Posté par
feralityre : disque chargé tournant 10-03-21 à 18:57

gts2 @ 10-03-2021 à 07:06

Bonjour,

Pour le 1), on ne peut utiliser le théorème d'Ampère : pas assez de symétrie pour trouver un parcours utile. Le résultat est correct.

Pour le 2, votre dq est en fait un d2q, vous avez une surface (deux dimensions, certains d'ailleurs notent cela d2S) et deux variables r et .  \dfrac{d^2q}{dt} = \dfrac{\sigma r d\theta dr}{dt} donne \sigma r\omega dr car \omega=\frac{d\theta}{dt}. Ceci étant cela marche par homogénéité, mais il faudra rédiger pour montrer que votre \dfrac{d^2q}{dt}   est bien un courant, c'est-à-dire une charge traversant une surface (en fait ici une ligne) par unité de temps.

Pour le 3, cela sera une simple intégration


Bonjour gts2, merci pour votre réponse,

d'accord donc si je comprend bien si je dérive quelque chose qui "contient " deux différentielles, cela donne le d^2 de cette chose ? C'est bien la même signification que la dérivée seconde ou pas ? Quelle est la règle générale à appliquer ?

Pour la 3 effectivement j'ai fait l'intégrale de 0 à R de dI (sommer les courants de toutes les spires de rayon entre 0 et R) et je trouve bien le résultat. Je vais faire la 4.

Posté par
feralityre : disque chargé tournant 10-03-21 à 18:58

J'ajoute que l'analyse dimensionelle de dI m'a donné la dimension de \dfrac{[C][r]}{[s]} or les radians [r] n'ont pas de dimension donc finalement juste \dfrac{[C]}{[s]} et c'est donc bien un courant.

Posté par
gts2re : disque chargé tournant 10-03-21 à 19:46

Citation :
si je dérive quelque chose qui "contient " deux différentielles, cela donne le d2 de cette chose ?

La notion d'homogénéité s'applique aussi aux différentielles, si vous dérivez une différentielle d'ordre deux , cela reste une différentielle d'ordre deux.
Mais ce n'est pas ce que vous avez fait : vous n'avez pas dérivé d2q (vous auriez trouvé zéro), c'est pour cela que j'ai dit qu'il fallait rédiger. Ce que vous avez calculé, c'est la charge qui traverse dr pendant dt, donc qui s'est déplacée de rdt, et la charge correspondante est d2q= dr rdt, le courant correspondant s'obtenant en "divisant" par dt.  

Citation :
c'est donc bien un courant

Vous avez raisonné par homogénéité et j'avais dit que, en effet, "cela marche par homogénéité", mais cela ne suffit pas : il est bien connu qu'un couple (en Nm) a même dimension qu'un travail, cela ne signifie par que si vous calculez un couple, vous avez calculé un travail. Votre résultat est exact, mais le courant ne s'obtient pas en dérivant la charge.

Posté par
feralityre : disque chargé tournant 10-03-21 à 20:13

D'accord... on pourrait peut être dire que d^2q est "la charge élémentaire" (comme c'est dit dans l'énoncé de la question), et dt un temps, cela fait "charge sur temps", et donc on a un courant ?

Posté par
gts2re : disque chargé tournant 10-03-21 à 20:19

Oui, mais dS n'est pas la surface autour du point M (r,), mais la charge qui s'est déplacée.

Posté par
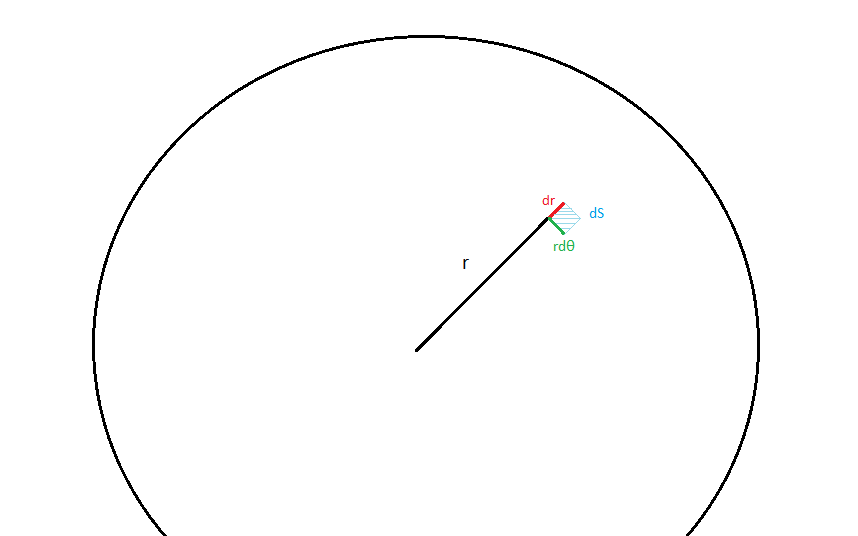
feralityre : disque chargé tournant 11-03-21 à 14:13

gts2 @ 10-03-2021 à 20:19

Oui, mais dS n'est pas la surface autour du point M (r,), mais la charge qui s'est déplacée.

Bonjour, désolé mais je ne suis pas sûr de bien comprendre... voici les choses que je comprends :

- dS = rdθdr , donc dS est la surface qui se trouve à la distance "r" du centre, de côté "radial" dr et de côté "orthoradial" rdθ (voir l'image).  " rdθ" est tellement petit qu'on ignore sa courbure, et donc dS est considéré comme un rectangle, d'aire dr\times rd\theta

- la charge qui est sur dS est d^2q.

Ensuite voici ce que je pense qui est à peu près juste :
Donc pour avoir le courant, on considère le déplacement de cette charge élémentaire d^2q, et on le trouve en dérivant par le temps car cela nous donne la vitesse angulaire fois
le rayon, qui est la vitesse en radians du cercle considéré.


Sinon pour la question 4 j'ai un peu bloqué... je pense que l'idée est d'intégrer le champ magnétique trouvé à la question 1 \vec{B(M)} entre 0 et R en considérant le R dans l'expression de \vec{B(M)} comme étant "r" et non plus "R" , et en remplaçant le "I" dans l'expression initiale de \vec{B(M)} par dI... ça semble la bonne approche ?

disque chargé tournant

Posté par
gts2re : disque chargé tournant 11-03-21 à 14:52

Bonjour,

Pour le 4, l'idée est la bonne, il ne reste plus qu'à intégrer !

Pour le 2, je pense que vous avez compris l'idée, il reste le problème de vocabulaire :  "et on le trouve en dérivant par le temps", on ne dérive pas par rapport au temps : vous avez calculé d2q la charge qui a traversé dr pendant dt et vous divisez par dt, vous n'avez pas dérivé d2q.

Posté par
feralityre : disque chargé tournant 12-03-21 à 19:14

gts2 @ 11-03-2021 à 14:52

Bonjour,

Pour le 4, l'idée est la bonne, il ne reste plus qu'à intégrer !

Pour le 2, je pense que vous avez compris l'idée, il reste le problème de vocabulaire :  "et on le trouve en dérivant par le temps", on ne dérive pas par rapport au temps : vous avez calculé d2q la charge qui a traversé dr pendant dt et vous divisez par dt, vous n'avez pas dérivé d2q.

Bonjour, d'accord je vois mieux. Désolé pour la lenteur mais j'avais d'autres travaux à rendre avant.

Pour la 4) j'ai utilisé la formule \vec{B(M)} = \dfrac{\mu_0 I}{2R}sin^3\alpha au lieu de  \vec{B(M)}=\dfrac{\mu_0 I R^2 \vec{u_z}}{2(R^2+z^2)^{3/2}} car je n'arrivais pas à intégrer sinon...

Avec cette première formule j'ai : \vec{B}=\dfrac{\mu_0}{2R}\vec{u_z}\int_0^R{(sin^3\alpha)\sigma\omega rdr} = \dfrac{\sigma\omega\mu_0(sin^3\alpha)R}{4}\vec{u_z}

Je crois que c'est faux car le résultat n'est pas homogène à l'unité du champ magnétique le Tesla...

Posté par
gts2re : disque chargé tournant 12-03-21 à 19:48

Bonjour,

Le passage en est une bonne idée, mais il faut aller jusqu'au bout : ne garder qu'une variable et ne pas considérer comme constant ce qui est variable.

Ici R (=r) est variable et sin() aussi.
Il faut donc se débarrasser de r par l'intermédiaire de tan().

Posté par
feralityre : disque chargé tournant 13-03-21 à 12:17

gts2 @ 12-03-2021 à 19:48

Bonjour,

Le passage en est une bonne idée, mais il faut aller jusqu'au bout : ne garder qu'une variable et ne pas considérer comme constant ce qui est variable.

Ici R (=r) est variable et sin() aussi.
Il faut donc se débarrasser de r par l'intermédiaire de tan().


Bonjour, d'accord je vois on doit considérer alpha comme étant la variable... Donc j'ai fait tan(\alpha)=\dfrac{r}{z} \quad; r=ztan(\alpha) \quad; \dfrac{dr}{d\alpha}=z(1+tan^2(\alpha)) \quad; dr = z(1+tan^2(\alpha))d\alpha

Et pour les bornes de l'intégrale, initialement étant de 0 à R, deviennent 0 et \arctan(\dfrac{R}{z}).

L'intégrale est : \vec{B}(M)=\dfrac{\sigma\omega\mu_0 z\vec{u_z}}{2R}\int_0^{arctan(\dfrac{R}{z})}sin^3\alpha(1+tan^2(\alpha))d\alpha

On a sorti "z" de l'intégrale car on calcule le champ magnétique à un point fixe de (Oz), qui ne bouge pas. C'est bien cette intégrale qu'il faut calculer ou je me suis trompé quelque part ?

Posté par
gts2re : disque chargé tournant 13-03-21 à 12:33

C'est la bonne direction.

Pour le calcul de l'intégrale  : 1+\tan^2(\alpha)=\frac{1}{\cos^2(\alpha)} est plus pratique.

Il n'y a pas de R au dénominateur (simplification avec le r de \sigma\omega rdr )  

Posté par
feralityre : disque chargé tournant 13-03-21 à 16:31

gts2 @ 13-03-2021 à 12:33


Il n'y a pas de R au dénominateur (simplification avec le r de \sigma\omega rdr )  


J'avais oublié de prendre en compte ce "r", il n'est pas dans mon intégrale finale je l'ai omis :/ pour moi cela devrait être un facteur r=ztan\alpha en plus dans l'intégrale du coup, je ne vois pas comment on pourrait le sortir en tant que "R".

Posté par
gts2re : disque chargé tournant 13-03-21 à 18:02

Vous l'avez "omis" avec raison puisqu'il se simplifie avec le r (et pas R) du dénominateur.
C'est plutôt ce R qu'il faut faire disparaitre.

Posté par
feralityre : disque chargé tournant 13-03-21 à 18:26

Désolé mais je ne vois aucun "r" dans un dénominateur dans les expressions qu'on a, j'ai beau regarder je ne vois pas comment le simplifier . Selon moi les "R" ne sont pas un problème car ils sortent simplement de l'intégrale.

Posté par
gts2re : disque chargé tournant 13-03-21 à 18:43

Quelle est la signification de R dans l'expression initiale de la question 1 ?
\vec{B(M)}=\dfrac{\mu_0 I R^2 \vec{u_z}}{2(R^2+z^2)^{3/2}} ou  \vec{B(M)} = \dfrac{\mu_0 I}{2R}sin^3\alpha

Quel est l'équivalent de ce R dans la question 4. Sachant que vous avez déjà répondu le  11-03-21 à 14:13 :

Citation :
en considérant le R dans l'expression de \vec{B(M)} comme étant "r" et non plus "R"

Posté par
feralityre : disque chargé tournant 13-03-21 à 19:04

Ah oui c'est vrai que j'avais dit ça... j'avais fait le raisonnement avec l'autre expression, et cette nouvelle expression avec "B(0)" j'ai eu du mal à voir que c'était la même chose au niveau du "R" qui passe en "r". D'accord donc je vois comment simplifier le "r", je vais faire l'intégrale qui paraît compliquée mais en cherchant un peu des astuces sur internet je devrais trouver .

Posté par
gts2re : disque chargé tournant 13-03-21 à 19:06

Pour l'intégration, la bonne variable c'est \cos(\alpha)

Posté par
feralityre : disque chargé tournant 13-03-21 à 21:29

Je trouve finalement \vec{B}=\dfrac{\sigma\omega\mu_0 z\vec{u_z}}{2}\left(\dfrac{(1+z+R)\sqrt{1+\dfrac{R}{z}}}{z+R}-2\right).  J'ai bien essayé de simplifier l'intégrale mais c'est la forme la plus simple que je trouve (je veux mettre la racine carrée au numérateur).

Posté par
feralityre : disque chargé tournant 13-03-21 à 21:32

(Je simplifie cos(arctan(\dfrac{R}{z}))=\dfrac{1}{\sqrt{(1+x)}} mais j'ai vu sur un site de calcul qu'ils faisaient cos(arctan(\dfrac{R}{z}))=\dfrac{z}{\sqrt{(z^2+R^2)}} je n'ai pas compris comment ça se fait)

Posté par
gts2re : disque chargé tournant 13-03-21 à 21:57

Je ne sais pas où vous avez trouvé votre première formule de cos(atan), mais elle est inexacte.

Il n'est pas nécessaire de calculer ce cos(atan) : vous avez besoin du cos de l'angle sous lequel on voit le disque depuis le point d'observation : la simple définition du cosinus (adjacent/hypoténuse) suffit. Quand vous indiquez les bornes de l'intégrale, indiquez plutôt que la valeur résultant du changement la valeur physique/géométrique voir symbolique \int_{centre}^{bord}

Je ne pense pas qu'il y ait de forme très simple.

Posté par
feralityre : disque chargé tournant 14-03-21 à 11:27

gts2 @ 13-03-2021 à 21:57

Je ne sais pas où vous avez trouvé votre première formule de cos(atan), mais elle est inexacte.

J'ai trouvé ça ici : https://socratic.org/questions/how-do-you-simplify-cos-arctan-x
et ici : https://openclassrooms.com/forum/sujet/cos-arctan-x . Leurs démonstrations semblent correctes pourtant mais ok tampis

gts2 @ 13-03-2021 à 21:57


Il n'est pas nécessaire de calculer ce cos(atan) : vous avez besoin du cos de l'angle sous lequel on voit le disque depuis le point d'observation : la simple définition du cosinus (adjacent/hypoténuse) suffit.

J'ai mis un moment à comprendre votre remarque mais je crois que j'ai compris ^^ en fait il ne faut pas utiliser arctan mais arccos, et au lieu de faire \alpha=arctan(R/z) comme les calculs diraient de la faire, il faut être utiliser arccos et faire \alpha=arccos(\dfrac{z}{\sqrt{z^2+R^2}}), de cette manière quand on prendra le cos de la borne supérieure, on annulera l'arccos et il restera juste \dfrac{z}{\sqrt{z^2+R^2}}

J'ai appliqué ça et le calcul de l'intégrale me donne : \vec{B}(M)=\dfrac{\sigma\omega\mu_0 z\vec{u_z}}{2}\left(\dfrac{z}{\sqrt{z^2+R^2}}+\dfrac{\sqrt{z^2+R^2}}{z}-2\right)

Posté par
gts2re : disque chargé tournant 14-03-21 à 11:40

Citation :
Leurs démonstrations semblent correctes pourtant


Socratic indique \cos(\arctan(\dfrac{R}{z}))=\dfrac{1}{\sqrt{1+x^2}} alors que vous écrivez : cos(arctan(\dfrac{R}{z}))=\dfrac{1}{\sqrt{(1+x)}}, ce n'est pas vraiment la même chose.

Sinon vous vous compliquez la vie : la variable étant   \cos \alpha, on obtient des termes du genre [\cos \alpha]_{centre}^{bord} et au bord \cos \alpha=\frac{adj.}{hyp.}=\frac{z}{\sqrt{z^2+R^2}}

Sinon le résultat final parait correct.

Posté par
feralityre : disque chargé tournant 14-03-21 à 15:28

D'accord merci !

Pour la 5) je dis que si on inverse le sens du courant \omega deviendra négatif car la rotation sera dans le sens anti-trigonométrique, donc le champ sera selon la composante -\vec{u_z}. Donc le sens du champ magnétique résultant sera inversé.

Pour la 6) je ne vois pas comment appliquer le DL proposé (1+x)^\alpha car "z" est présent à 5 endroits, des fois sous une racine et au carré, des fois non... je ne vois pas comment m'y prendre.

Posté par
gts2re : disque chargé tournant 14-03-21 à 15:50

Il doit y avoir une faute de frappe : z étant grand, il faut faire intervenir 1/z et un DL devant se faire vis-à-vis d'une grandeur sans dimension, le DL est donc un DL en (R/z).

Je suppose que vous connaissez les étapes : faire apparaitre ce (R/z), puis DL à l'ordre 2 des deux racines (ordre 2 puisque la dépendance est déjà en (R/z)2).

Posté par
feralityre : disque chargé tournant 14-03-21 à 17:24

D'accord donc j'ai fait le calcul et je trouve finalement : \vec{B}(M) = \dfrac{\sigma\omega\mu_0 \vec{u_z}R^4}{4z^3} .

Pour la 7) j'applique la formule du moment magnétique \vec{M} = I\vec{S}, avec d'après la question 3) I=\dfrac{\sigma\omega R^2}{2} donc \vec{M} = \dfrac{\sigma\omega R^4\pi}{2}

Posté par
gts2re : disque chargé tournant 14-03-21 à 17:53

Je trouve presque pareil (mais je peux me tromper...)

\vec{B}(M) = \dfrac{\sigma\omega\mu_0 \vec{u_z}R^4}{8 z^3}
Le 8 venant de 1/2 initial, x 2 (les deux fonctions), x1/8 (DL ordre 2)

Idem pour le moment  M = \dfrac{\sigma\omega R^4\pi}{4} par intégration des moments élémentaires \sigma \omega r \rm{d} r \pi r^2, le votre correspond à un courant I circulant à la périphérie du disque.

Posté par
feralityre : disque chargé tournant 14-03-21 à 18:11

gts2 @ 14-03-2021 à 17:53

Je trouve presque pareil (mais je peux me tromper...)

\vec{B}(M) = \dfrac{\sigma\omega\mu_0 \vec{u_z}R^4}{8 z^3}
Le 8 venant de 1/2 initial, x 2 (les deux fonctions), x1/8 (DL ordre 2)

Idem pour le moment  M = \dfrac{\sigma\omega R^4\pi}{4} par intégration des moments élémentaires \sigma \omega r \rm{d} r \pi r^2, le votre correspond à un courant I circulant à la périphérie du disque.

Ah oui vous avez raison j'ai oublié le 1/2 qui était déjà au dénominateur, c'est bien 8 au dénominateur, je suis étourdi. Merci ! La 8 semble être un calcul assez simple, je dirai ce que j'obtiens.

Posté par
feralityre : disque chargé tournant 14-03-21 à 18:26

Ah mais donc mon approche pour le moment n'est pas bonne ? Pourtant I est le courant total dans tout disque... étant donné qu'on se trouve très loin ça pourrait être une approximation acceptable ? Ou il faut forcément intégrer les moments élémentaires comme vous avez fait ?

Posté par
gts2re : disque chargé tournant 14-03-21 à 18:35

Je reprend la question 2 : le courant élémentaire à une distance r est \rm{d}I=\sigma r\omega \rm{d} r et correspond à une surface S=\pi r^2 et donc à un moment dM=S \rm{ d}I

Posté par
feralityre : disque chargé tournant 14-03-21 à 18:38

gts2 @ 14-03-2021 à 18:35

Je reprend la question 2 : le courant élémentaire à une distance r est \rm{d}I=\sigma r\omega \rm{d} r et correspond à une surface S=\pi r^2 et donc à un moment dM=S \rm{ d}I


D'accord oui j'ai calculé le moment en intégrant (je trouve pareil que vous) puis fait la question 8 et on retrouve bien le résultat de la question 6

Merci beaucoup gts2 je n'y serais jamais arrivé sans votre aide


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !