Niveau maths spé

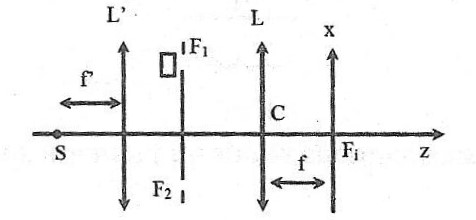
dispositif à DFO

Posté par
iSirrol 22-01-16 à 17:59

bonjour
dispositif à DFO $a=F_1F_2$
j'ai établi que la différence de marche s'écrit $\delta '=\delta+(n-1)e=\frac{a(x-x_0)}{f'}$ où j'ai posé $x_0=\frac{(1-n)ef'}{a}$
on me demande de déterminer le nombre $N$ de franges qui ont défilées, j'ai dit que c'était $\frac{x_0}{i}$ or je n'ai aucune idée de comment trouver l'interfrange $i$
je sais que de manière générale on a $\Phi=\frac{2\pi X}{i}$ au quel cas il est facile de trouver l'interfrange mais là c'est plus compliqué

Posté par re : dispositif à DFO 22-01-16 à 18:23

Bonsoir,
tu sembles avoir compris ce qui se passe mais tu es un peu maladroit au niveau de la technique de calcul.
Sans la lame, tu as :

$\delta=L_{2}-L_{1}=\frac{a.x}{f'}$

$\\ \text{franges brillantes : \ensuremath{\delta=k.\lambda\quad avec\;:\; k\in\mathbb{Z\quad\text{ordre d'interférence}}}}$

$\\ \text{\text{abscisses des franges brillantes : \ensuremath{x_{b}=k\frac{\lambda.f'}{a}}}}$
En présence de la lame, la longueur du chemin optique n° 1 augmente de (n-1)e ; le calcul précédent est modifié ainsi :

$\\ \delta=L_{2}-(L_{1}+e\left(n-1\right))=\frac{a.x}{f'}-e\left(n-1\right)$

$\\ \text{franges brillantes : \ensuremath{\delta=k.\lambda\quad avec\;:\; k\in\mathbb{Z\quad\text{ordre d'interférence}}}}$

$\text{\text{abscisses des franges brillantes : \ensuremath{x_{b}=k\frac{\lambda.f'}{a}+\frac{e\left(n-1\right).f'}{a}}}}$

On remarque que l'interfrange n'est pas modifié, le système de frange ayant subit une translation verticale vers le haut si la lame est placée devant la fente la plus haute, vers le bas si la lame est placée devant la fente la plus basse.

Posté par re : dispositif à DFO 22-01-16 à 22:33

merci
oui mais du coup comment trouver $N$

Posté par re : dispositif à DFO 23-01-16 à 16:41

Bonjour,
Le déplacement vers le haut du système de frange est :

$\triangle x=\frac{e\left(n-1\right)f'}{a}$
alors que l'interfrange vaut :

$i=\frac{\lambda f'}{a}$
Tu as donc :

$N=\frac{\triangle x}{i}=\frac{e\left(n-1\right)}{\lambda}$
Attention à bien interpréter la partie fractionnaire de N !

Posté par re : dispositif à DFO 24-01-16 à 13:32

merci je vois mieux maintenant avec un peu plus de pratique

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

dispositif à DFO

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique