Bonjour
En toute rigueur, une distribution surfacique, cela n'existe pas : il s'agit d'une distribution volumique  de très faible épaisseur "e". Si on fait tendre "e" vers zéro tout en maintenant =.e fixe, on obtient effectivement une discontinuité. C'est donc la modélisation surfacique, simplification de la réalité qui introduit cette discontinuité.
Evidemment, on peut retrouver cela mathématiquement à partir de la divergence du vecteur E.

Excuser moi mais je n'arrive pas à imaginer cette discontinuité
est ce qu'on peut la demontrer par un schemas

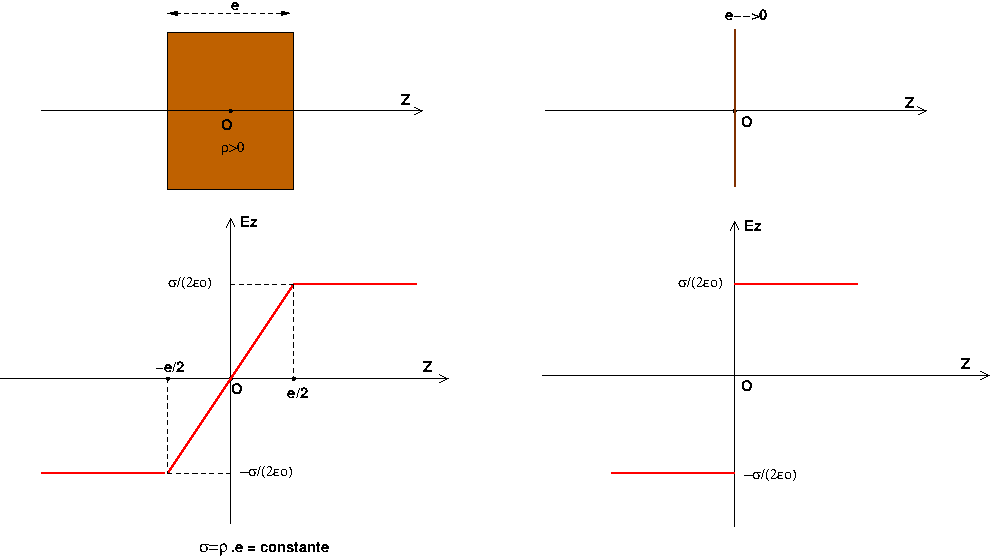
J'ai imaginé le cas simple d'une plaque d'épaisseur e de longueur et de largeur infinies pour obtenir un résultat simple. La plaque est uniformément chargée en volume. Le vecteur champ dans ce cas ne dépend que de z et est perpendiculaire à la plaque. J'ai représenté les variations de la composante Ez de E (la seule composante non nulle) en fonction de z. Imagine que l'on diminue l'épaisseur e de la plaque en maintenant le produit .e= fixe tout en faisant tendre e vers zéro. On fait apparaître une discontinuité de Ez égale à /_o (figure de droite).
Pour une distribution linéique : il faut imaginer un cylindre de rayon R uniformément chargé en volume. En supposant pour faire simple, le cylindre de longueur infinie on obtient pour le vecteur champ radial une composante Er fonction continue de r : la distance à l'axe du cylindre. Er augmente en fonction de r pour r<R puis diminue ensuite...

merci  infiniment vanoise  tes   explication sont bien détaillée s