Inscription / Connexion Nouveau Sujet
Dipôle électrique dans une sphère
Bonjour j'ai à faire à un exercice dont je ne sais pas par où commencer.
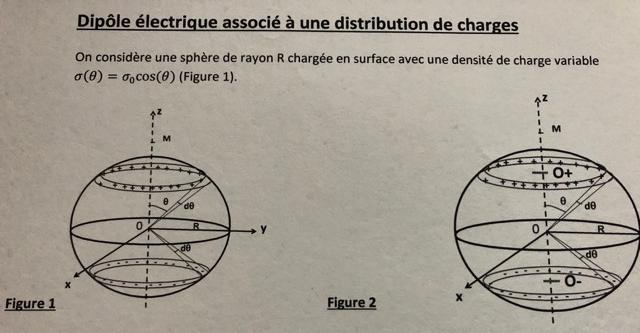
J 'ai une sphère de rayon R chargée en surface avec une densité de charge variable σ(θ)= σ(0)cos(θ)
1) Je dois trouver l'expression du vecteur moment dipolaire électrique contitué de deux charges +Q et -Q de distance L
2) Également déterminer les charges (+dQ) portée par la bande chargée de centre O+, de rayon r=Rsinθ et de largeur Rdθ et (-dQ) portée par la bande chargée (-) de centre O-
Si quelqu'un peut m'aiguiller , merci.
Bonjour
Pour la 1), il s'agit sans doute de rappeler l'expression du moment dipolaire de ton cours. Soit une charge ponctuelle Q en P et une charge négative ponctuelle au point N. Par définition : le moment dipolaire est :
Pour la deux : la surface élémentaire de la couronne élémentaire est :
dS=2 .r.R.d
.r.R.d
La charge de cette couronne est donc :
dQ= .dS
.dS
Je te laisse remplacer  et r par leurs expressions en fonction de
et r par leurs expressions en fonction de  .
.
L'intégration entre 0 et  /2 va te fournir la charge Q de l'hémisphère nord.
/2 va te fournir la charge Q de l'hémisphère nord.
L'intégration de  /2 à
/2 à  va te donner la charge de l'hémisphère sud. Tu devras vérifier que ces deux charges sont opposées.
va te donner la charge de l'hémisphère sud. Tu devras vérifier que ces deux charges sont opposées.
Pour la un j'ai mis p=Q.L dans ce cas , à moins que je ne laisse sous la forme vectorielle /+Q-Q ?
Pour la 2 j'ai fait ce qu'il y a en dessous :
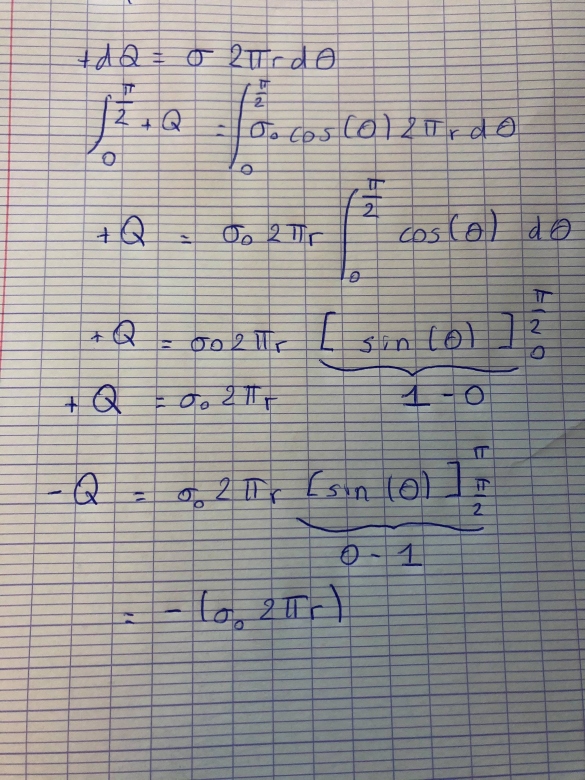
Pour 1) ton énoncé parle de vecteur.
Pour 2) ton résultat est nécessairement faux car il n'est pas homogène : une charge électrique est homogène à une densité surfacique multipliée par l'aire d'une surface et non multipliée par une distance. Reprends pas à pas mes indications de mon précédent message. Tu vas logiquement te retrouver à prendre une primitive de :
2.sin( ).cos(
).cos( )=sin(2
)=sin(2 ).
).
Bonsoir,
@Nestaty : pour éviter d'alourdir les serveurs avec des images scannées, tu as deux utilitaires proposés pour écrire une formule mathématique :
 extrait de
extrait de Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?

Excusez moi pour les images ...
Merci beaucoup! J'ai encore une petite question si tu peux m'aider...
/ En assimilant chaque bande chargée + et - avec sa charge +dq et -qd déterminer le vecteur moment dipolaire électrique dp associé aux deux bandes chargées, en déduire le vecteur moment dipolaire associé à la sphère de densité σ(θ)= σ(0)cos(θ).
Je n'ai pas vu les moments dipolaires en cours je bute donc un peu sur ces questions...
Edit : dois-je reprendre la formule p=q.NP avec NP le vecteur entre les deux charges +Q et -Q c'est à dire remplacer NP comme vecteur entre les deux points -Q = sigma(0) R² * pi et +Q l'opposé
Si tu appliques la formule que je t'ai fournie au dipôle élémentaire, le moment dipôlaire élémentaire s'écrit :
Tu remplaces dQ par son expression déjà utilisée et tu intègres entre 0 et  .
.
en remplacant sans intégrer , me suis-je trompé ?
dp= 4
4 ^3sin(
^3sin( )cos(
)cos( ) d
) d
en remplacant le sigma j'obtiens un autre cos
super merci je trouve p=-4 R^3
R^3 (0)
(0)
concernant l'expression du champ électrique assimilé à un dipole j'ai mis
E(M)=p/2
 (0)r^3 selon uz
(0)r^3 selon uz
est-ce correct ?
Concernant le moment dipolaire :
il est conventionnellement orienté des charges - vers les charge + donc suivant Oz.
Quelles bornes d'intégrations as-tu choisies ? Manque un 3 au dénominateur.
d'où vient cette expression du vecteur champ ?
Merci pour la précision,
J'ai regardé sur certains forum , il passent par le potentiel dipolaire V puis avec E(M)=-gradV on déduit l'expression, mais je n'ai pas bien compris, je pense qu'il y a plus facile pour trouver l'expression du champ électrique
quelle est l'expression du champ électrique crée par la sphère chargée assimilée à un dipole électrique ?
Il n'est pas précisé en quel point ? La méthode que tu as vue sur le net n'est valide qu'à des distances de la sphère très grandes devant le rayon R. Peux-tu fournir l'énoncé intégral ?
A ce que je comprends, c'est la question B6 qui te pose problème. Je pense qu'il faut se limiter comme à la partie A au potentiel et au vecteur champ en M en faisant intervenir sa cote z. Si on se limite ainsi aux points sur l'axe (Oz), il n'est pas nécessaire de supposer |z| très grand devant R. Tu peux rechercher l'expression de V(M) puis écrire :
Je trouve des formules pour le potentiel tel que :
V(M) = -q/(4.
 .0.NM) + -q/(4.
.0.NM) + -q/(4.
 .0.PM) N étant la charge - et P la charge + et un M un point aux coordonnées sphériques , est-ce utilisable ?
.0.PM) N étant la charge - et P la charge + et un M un point aux coordonnées sphériques , est-ce utilisable ?
Ton énoncé n'est pas clair mais, selon la figure 2, il est possible qu'il s'agisse seulement de trouver le potentiel et le vecteur champ en un point M de l'axe (Oz). Dans ce cas, les coordonnées sphériques sont inutiles.
Il faut être rigoureux dans les notations. L'énoncé demande de noter Q et -Q les deux charges, pas q et -q.
Puisque : p=Q.NM et que tu connais les expressions de Q et de p, tu peux facilement obtenir les cotes des points M et N sachant que le milieu du segment NM est le centre O de la sphère. Tu obtiendras alors en fonction de z, les distances MN et MP nécessaires pour exprimer le potentiel en M.

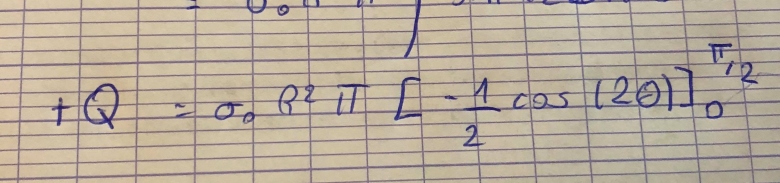
 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum [/smb]
[/smb]
