Inscription / Connexion Nouveau Sujet
Diode a jonction PN
salut cher(e) physicien(ne) je vous remercie toujours pour votre aide et vos intervention sur mais problèmes qui m'ont tellement aidé et aujourd'hui j'ai juste une petite question concernant un exo que je vais le presenter ci-dessous .
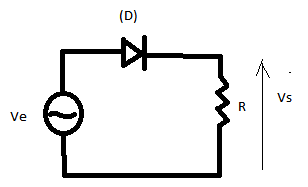
On considère le circuit représenté dans la figure ci-dessous comprtant une diode (D) en serie avec une resistance R=100(ohm)alimentées par un générateur de tension sinusoidale Ve=12sin(2πft) avec f=50Hz
a) D possede une resistance nulle et une tension seuil égale a 0.6V
b) D possede une résistance de 10(ohm) et une seuil égale a 0.6V.
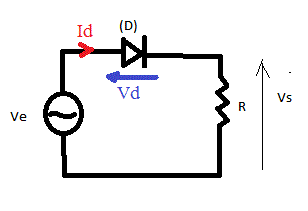
1) Donner les équations de variations de Id(t),Vd(t) et Vs(t).
2) tracer les courbes Ve(t),Id(t),Vs(t)et Vd(t) pour chaque cas (a et b).
*** pour moi la 1ère queestion où j'ai un petit problème : normalement on va calculer Id(t) comme etant une equation de droite de charge , mais pour Vd(t) est ce qu'on va annuler Id(t) pour obtenir Vd(t) dans la droite de charge (càd:Id=(Ve-Vd)/R <=> Vd=Ve )ou bien on remplace Id par sa valeur dans l'equation de la diode (Vd=rd*Id+Vseuil <=> Id=(Vd-Vseuil)/rd )????
attend vos reponses evec impatience et merci ...
Bonsoir,
Quelques indications pour le a.
On peut toujours écrire ve-uD -vs = 0
Si la diode est passante ve>= 0,6 V et uD= 0,6 V alors vs= ve - 0,6 V
Si la diode est bloquée alors vs = R*i = 0
A vous lire. JED.
JED le a) et b) ne sont pas des question ce sont des cas où le diode soit il est de resistance null ou bien un recepteur qui a une resistance non-null .
1)
a)
Etude sur une période du signal d'entrée.
Ve = 12.sin(314.t)
Pour Ve <= 0,6 V (diode bloquée), soit donc pour t (en s) dans [0 ; 1,59.10^-4] U [9,84.10^-3 ; 20.10^-3] :
Id(t) = 0
Vd(t) = Ve = 12.sin(314.t)
Vs(t) = 0
---
Pour Ve > 0,6 V, soit donc pour t (en s) dans ]1,59.10^-4 ; 9,84.10^-3[
Id = (ve - 0,6)/R
Vd(t) = 0,6 V
Vs = R*Id = R * (12.sin(314.t) - 0,6)/R
-----
b)
Pour Ve <= 0,6 V (diode bloquée), soit donc pour t (en s) dans [0 ; 1,59.10^-4] U [9,84.10^-3 ; 20.10^-3] :
Id(t) = 0
Vd(t) = Ve = 12.sin(314.t)
Vs(t) = 0
---
Pour Ve > 0,6 V, soit donc pour t (en s) dans ]1,59.10^-4 ; 9,84.10^-3[
Id = (ve - 0,6)/(R+r) (Avec r = 10 ohms la résistance de la diode)
Vd(t) = 0,6 + r.Id = ...
Vs = R*Id = R*(ve - 0,6)/(R+r) = R * (12.sin(314.t) - 0,6)/(R+r)
-----
Sauf distraction. Vérifie. 
b)
Pour Ve > 0,6 V, soit donc pour t (en s) dans ]1,59.10^-4 ; 9,84.10^-3[
Id = (ve - 0,6)/(R+r) (Avec r = 10 ohms la résistance de la diode)
Vd(t) = 0,6 + r.Id = ...
ici qd on remplace Vd=r*Id+0.6 cela donne le point de fonctionnement de la diode et non pas Id en fct de t ...
n'est ce pas ?!
b)
Pour Ve > 0,6 V, soit donc pour t (en s) dans ]1,59.10^-4 ; 9,84.10^-3[
Id = (ve - 0,6)/(R+r)
et donc : Id(t) = (12.sin(314.t) - 0,6)/(R+r)
Id(t) = (12.sin(314.t) - 0,6)/110
Qui est bien l'expression de Id en fonction de t.
-----
Sauf distraction. 
oui c'est bien j'ai compris merci 
alors que pour tracer Id(t) il faut que Vd soit null et donc Id(t)=Ve/R
car Id=f(Vd,t) donc pour passer a deux dimension il faut que Vd=0 (= sachant que tout les courbe ont la meme pente (1/R) donc sont tous parallele )
cela est juste ? J-P 
Vd n'est jamais nul sauf très ponctuellement. (aux passages par 0 de Ve)
Si la diode est passante, Vd = 0,6 V (+ éventuellement la chute dans sa résistance série interne) et si elle est bloquée, la tension Vd varie (dans le cas de l'exercice) depuis (-12 V jusque + 0,6 V)

oui je sais que Vd n'est pas null
j'ai voulu dire pour tracer Vd(t) il faut passer de 3Dimension vers 2Dimension
donc donc dans l'expression de la droite de charge Id(t)=(Ve-Vd)/R devient Vd(t)=Ve
est ce vrai ??? 
pourtant c'est ce que notre prof nous a dit 
Qu'est ce que tu racontes ?
On est toujours en "2 dimensions" pour tracer les courbes demandées.
La courbe de Vd(f) se fait dans un repère avec Vd en ordonnées et t en abscisse.
-----
exemple pour le cas b
Vd(t) = 12.sin(314.t) pour t(en s) dans [0 ; 1,59.10^-4] U [9,84.10^-3 ; 20.10^-3]
et pour t dans ]1,59.10^-4 ; 9,84.10^-3[ s
Vd(t) = 0,6 + r.Id
Vd(t) = 0,6 + 10.Id
Vd(t) = 0,6 + 10.(12.sin(314.t) - 0,6)/110
Vd(t) = 0,6 + (12.sin(314.t) - 0,6)/11
On peut donc facilement tracer la courbe de Vd(t)
Cela donne ceci :
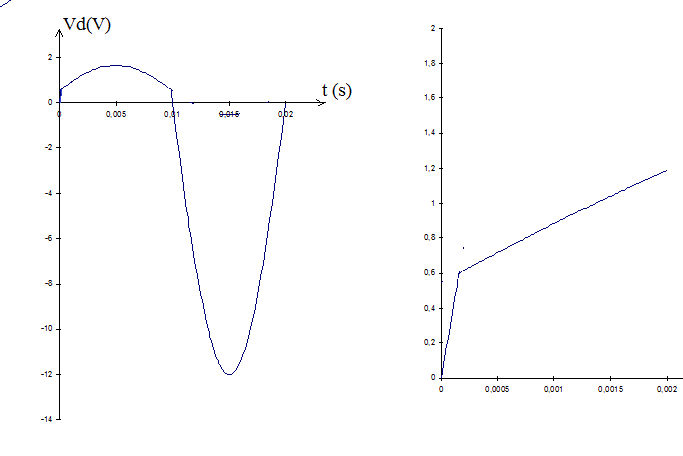
A gauche, une période entière représentée.
A droite, un "zoom" sur le début de courbe.
Sauf distraction. 




