Niveau licence

Dimension transverse d'un faisceau lumineux

Posté par
Syrocco 23-09-19 à 21:59

Bonjour,

j'essaye de résoudre un exo qui ne me semble pas très clair.

Dans l'espace libre, une onde optique de pulsation $\omega$ est formée d'une superposition à poids égaux d'ondes planes progressives de même pulsation.

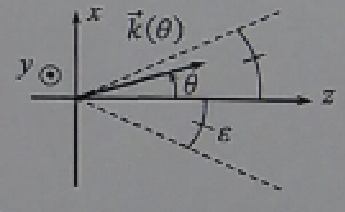
On définit:
$\vec{k}=k_0cos(\theta)\vec{e_z}+k_0sin(\theta)\vec{e_x}$ avec $\theta < \epsilon <<1$ .

On a $E_y=E_0\int_{-\epsilon}^{\epsilon}\mathrm{d}\theta e^{i(k_0cos(\theta)z +k_0sin(\theta)x-\omega t)}$
L'onde est polarisée linéairement selon y.

Question 1: En utilisant $\vec{k}$ exprimé à l'ordre 1, montrer que l'onde possède une extension transverse $\Delta x=\dfrac{\pi}{\epsilon k_0}$ .

Réponse: $\Delta x=\Delta \lambda_x=\dfrac{2\pi}{\Delta k_{xMax}}$ . Je fais le dev. limité de k: $k_x=k_0\theta$ et je le prend en $\epsilon$ j'obtiens donc: $\Delta x=\dfrac{2\pi}{k_0\epsilon}$ mais il me manque un facteur 1/2 alors qu'au contraire, j'aurai été tenté de mettre un facteur 2 pour prendre en compte la partie inférieur du schéma (c'est à dire l'onde en $-\epsilon$ ).

Question 2: En poussant le développement limité jusqu'à l'ordre 2, montrer que l'onde possède également une divergence aux grands z.

Réponse: Le développement limité donne $\vec{k}=k_0(1-\dfrac{\theta ^2}{2})\vec{ez}+k_0\theta\vec{ex}$ . Mais je ne sais absolument pas quoi faire ensuite. La question me parait triviale puisque le vecteur d'onde part vers + l'infini....

Merci d'avance pour vos réponses et bonne soirée!

$Dimension transverse d\'un faisceau lumineux$