Inscription / Connexion Nouveau Sujet
Difficulté pour établir une équation différentielle
Bonjour.
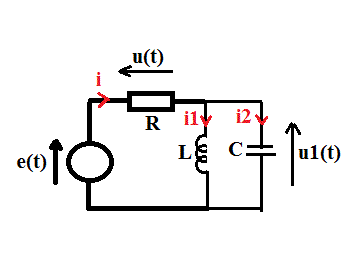
J'ai un circuit électrique (désolée je ne peux pas joindre d'image) composé de deux mailles telles que :
branche la plus à gauché un générateur de tension produisant une tension e(t)=Ecos( t), en haut, une résistance dont la tension à ses bornes est u(t) (à déterminer), branche du milieu, une bobine d'inductance L et branche de droite, un condensateur de capacité C.
t), en haut, une résistance dont la tension à ses bornes est u(t) (à déterminer), branche du milieu, une bobine d'inductance L et branche de droite, un condensateur de capacité C.
J'ai essayé d'établir les lois des mailles :
e=u+uL et e=u+uC mais viennent alors s'ajouter les intensités, et je ne m'en sors pas.
Avez-vous une bonne méthode pour réussir à traiter un tel exercice ?
Merci beaucoup pour vos explications.
Es-tu bien sûr que c'est l'équation différentielle que tu dois trouver ?
... car ce n'est pas nécessaire si on veut trouver l'expression de u(t) en régime permanent.
(C'est alors plus facile par la détermination de l'impédance complexe vue par le générateur ... suivie d'une manipulation facile)
-----
Si c'est vraiment l'équation différentielle de u(t) que tu veux :
u1 + u = E.cos(wt)
u = R.i
i2 = C.dU1/dt
u1 = L.di1/dt
i = i1 + i2
On élimine u1 :
L.di1/dt + u = E.cos(wt)
u = R.i
i2 = LC . d²i1/dt²
i = i1 + i2
On élimine i2 :
L.di1/dt + u = E.cos(wt)
u = R.i
i = i1 + LC.d²i1/dt
On élimine i :
L.di1/dt + u = E.cos(wt) --> di1/dt = E.cos(wt)/L - u/L
u/R = i1 + LC.d²i1/dt --> du/dt = R.di1/dt + RLC.d³i1/dt²
d²i1/dt² = -E.w.sin(wt)/L - 1/L. du/dt
d³i1/dt³ = -E.w².cos(wt)/L - 1/L. d²u/dt²
du/dt = R.(E.cos(wt)/L - u/L) + RLC.(-E.w².cos(wt)/L - 1/L. d²u/dt²)
du/dt = R.E.cos(wt)/L - R.u/L - RC.E.w².cos(wt) - RC. d²u/dt²
RC. d²u/dt² + du/dt + (R/L).u = E.cos(wt) * (R/L - RC.w²)
d²u/dt² + (1/(RC)).du/dt + (1/(LC)) * u = E.cos(wt) * ( 1/(LC) - w²)
d²u/dt² + (1/(RC)).du/dt + (1/(LC)) * u = E.cos(wt) * ( 1 - w²LC)/(LC)
-----
Sauf distraction (Non vérifié).

Merci beaucoup pour tes explications très complètes !
J'avais trouvé finalement en faisant autrement, en dérivant e(t) tout de suite (mais je ne sais pas si on pouvait le faire... et finalement si !). J'arrivais bien à :
e = u + L d/dt (u/R - C d/dt (e-u)) et après supplication, tout s'arrange bien.
Autre question sur un sujet qui revient souvent : je décide ensuite de trouver l'amplitude Um du signal donc je passe en complexes. Je pose  02 = 1/LC et Q=
02 = 1/LC et Q= 0/(1/RC)) et j'arrive à ça pour simplifier :
0/(1/RC)) et j'arrive à ça pour simplifier :
u'' +  0/Q u' +
0/Q u' +  02 u = E*cos(
02 u = E*cos( t)(
t)( 02-
02- 2) puis je passe dans
2) puis je passe dans  et j'ai :
et j'ai :
u(- 2+
2+ 02+
02+ 0/Q j
0/Q j )=Ecos(
)=Ecos( t)(
t)( 02-
02- 2)
2)
Et finalement :
u = Ecos( t)(
t)( 02-
02- 2) / (-
2) / (- 2+
2+ 02+
02+ 0/Q j
0/Q j )
)
Ensuite, pas de problème, je calcule le module.
Est-ce correct ?


