Inscription / Connexion Nouveau Sujet
Diagramme énergétique
Bonjour à tous  ,
,
Voici un des exercices que j'ai à faire:
"On considère un point matériel M qui se déplace sans frottement sur un axe horizontal Ox fixe. On associe au système {axe Ox, M } une énergie potentielle d'interaction notée U(x). "
1) Quelle est la direction de la force agissant sur M? Donner son expression vectorielle.
2) Qu'appelle-t-on position d'équilibre, stable ou instable du système ?
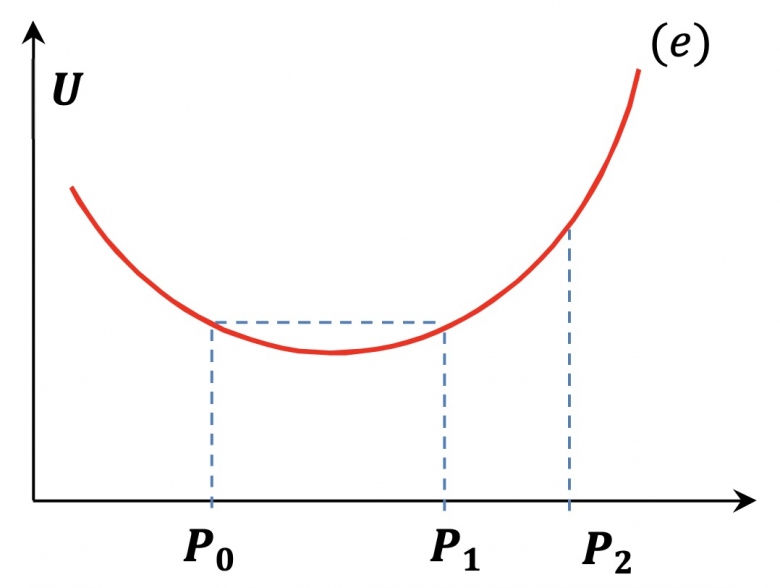
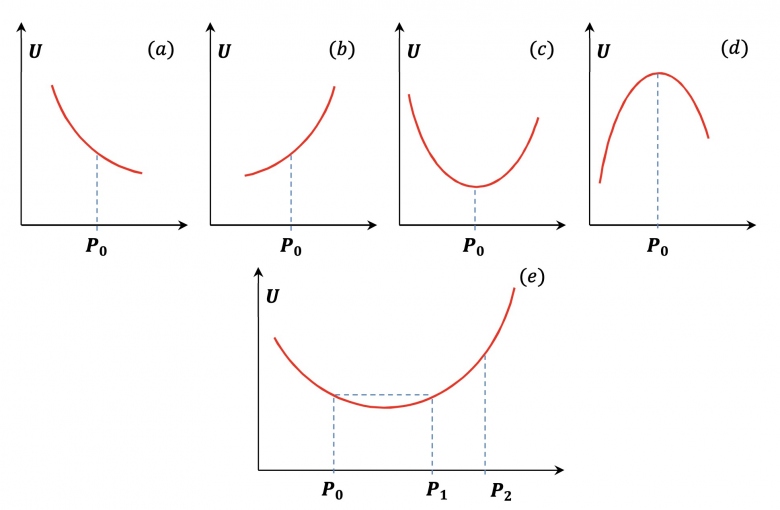
3) À l'instant t = 0, M est lâché sans vitesse initiale en un point P0 de coordonnée x0. Indiquer qualitativement quel sera le mouvement ultérieur du point M pour chacune des figures suivantes donnant l'allure de la variation de U(x) au voisinage de P0. Dans le cas de la figure (e), le point P2 est-il accessible à M?
Malheureusement, je bloque déjà sur la question 1:
Je ne comprends pas pourquoi on nous demande quelle est LA force.
En effet, selon moi, il y a deux forces agissant sur M en absence de frottement:
-Le poids P
-La réaction du sol N.
Est-ce une erreur d'énoncé ou est-ce bien moi qui suis sur la mauvaise piste? ^^
Bonjour,
Vous avez raison, mais ce n'est pas vraiment une erreur d'énoncé, plutôt un manque de précision : F est la force dérivant de l'énergie potentielle U.
Ce serait donc l'énergie potentielle de pesanteur avec P comme force?
Ce que je ne comprends pas c'est comment P peut induire un mouvement de M alors que P est perpendiculaire à la trajectoire ^^
Si je comprends bien, on a:
F = dEp/dx
Est-ce bien cela?
Cependant, comment connaître la direction et l'expression vectorielle de cette force?
Je crois avoir compris,
Je pense que F est colinéaire à Ox et donc son expression vectorielle est F = F Ux
Est-ce bien cela?
Pour la question 2, c'est du cours.
Une position d'équilibre est une position telle que si on lâche le système sans vitesse dans cette position alors il reste immobile. (La résultante des forces est nulle).
Équilibre stable: si on écarte légèrement le système de cette position, alors il tend naturellement à y revenir. (U est minimale)
Équilibre instable : si on écarte légèrement le système de cette position, alors il tend naturellement à s'en écarter encore plus. (U est maximale)
Pour en venir au corps de l'exercice, la question 3:
Figure a) :
Il n'y a pas d'équilibre car U(x0) n'est ni un maximum, ni un minimum.
Par contre, je bloque un peu sur le mouvement, je ne sais pas vraiment si M part à gauche ou à droite ^^
Bonjour,
Un raisonnement intuitif consiste à considérer que l'axe vertical est l'altitude z (donc à un coefficient près l'énergie potentielle de pesanteur mgz), et que la courbe représente l'altitude du sol. On a donc Ep au sol fonction de la position. Que ferez une bille placée au sol dans les 5 cas ?
Plus formel, quel est le signe de F au point P0 ?
Le signe de F est l'opposé du signe de dU/dx. Pour la figure a, la tangente en x0 a un coefficient directeur négatif. Donc le signe de dU/dx est négatif. Ainsi, le signe de F est positif. Ce qui impliquerait que M se déplace vers la droite ?
Donc pour la figure b:
M va se déplacer vers la gauche.
Pour la figure c:
C'est un minimum donc équilibre stable. Faut-il dire que le point M ne va pas tout simplement pas bouger ou faut-il dire qu'il va bouger et revenir à sa position initiale x0?
Je pencherai plus pour la réponse suivante: il ne va pas bouger car c'est un équilibre stable et M est lâché sans vitesse initiale.
La réponse pour laquelle vous penchez est la bonne.
La phrase d'avant permet de préciser la notion de stabilité, si on perturbe un peu, il tend à revenir en P0, tend car sans frottement, M va osciller.
J'ai un peu plus d'hésitation pour la figure d:
C'est un maximum donc équilibre instable.
Cependant, si M est uniquement lâché à P0 et non écarté de sa position, M va -t-il bouger?
De plus, si M viendrait à bouger, comment pouvons nous savoir dans quelle sens il bougerait?
Bonjour,
Si M est strictement en P0, il ne bouge pas. Mais que veut-dire strictement ?
De manière idéale, cela voudrait dire que x(M)-x(P0)=0,0000 m avec une infinité de zéro après la virgule...
Donc on ne sera jamais strictement en P0, donc M va s'écarter de P0, mais dans un sens qui va dépendre du fait que l'écart soit de 0,0000001 ou -0,00000001
D'accord, tout se joue sur les mots si je comprends bien. Je vais être très précis dans ma rédaction.
Quand à la figure e:
La dérivée de U(x0) est négative donc M va se déplacer vers la droite. Cependant, quelles informations devons-nous utiliser pour déterminer si M atteint x2 (P2) ?
D'ailleurs, je me demande pourquoi x1 (P1) a été indiqué sur la figure. Est-ce parce que l'énergie potentielle ne peut pas être plus élevé qu'a t = 0 ?
Je crois avoir compris mais je suis pas certain.
On suppose que F est une force conservative. Alors l'énergie mécanique du système est constante.
M est lâché sans vitesse initiale à x = x0. Donc on a Em(x0) = U(x0)
En arrivant à x = x1, on a U(x1) = U(x0). Donc, à partir de ce moment là, l'énergie potentielle ne peut plus augmenter car est toujours U(x) <= Em(x), c'est l'énergie cinétique qui va augmenter.
Cependant, ce qui me chagrine c'est que je suppose que la force F est conservative.
Auriez-vous des conseils quant à cela?
Pour e) il faut penser à l'hypothèse "sans frottement" qui implique ?
Pour la rédaction de d), cela dépend un peu de votre cours...
Pour la e:
Je comprends bien qu'il n'y a pas de frottements.
Cependant, comment peut-on prouver que la force F est conservative?
C'est vrai que l'énergie potentielle est associée à certaines forces uniquement. Ces forces en question sont les forces conservatives. Est-ce bien cela?
Donc l'énergie mécanique est constante et U(x) <= Em(x)
M étant lâché sans vitesse initiale, Em(x0) = U(x0)
D'après la figure, on a: U(x1) = U(x0)
Donc: Em(x1) = U(x1)
Ainsi, le point P2 n'est pas accessible à M.
De manière plus intuitive, M va oscillé entre P1 et P2 jusque s'immobiliser au minimum que l'on a entre P1 et P2.
Est-ce correct?
C'est bien compris.
Remarque de rédaction, le fait que M s'immobilise suppose qu'il y a des frottements.
C'est vrai que je n'y avais pas pensé. Devrais-je plutôt dire "tend vers le minimum qu'il y a entre P0 et P1" ?
Si on suit le texte à la lettre, je ne garderai que le début de la phrase :
"M va osciller entre P0 et P1"
Manifestement, la physique est comprise, vous buttez plutôt sur des problèmes d'interprétation d'énoncé.
Bonjour,
Une question m'est venue en rédigeant.
Faut-il supposer, en début d'exercice, que M va bouger vers la droite quand F est positif et vers la gauche quand M est négatif?
Ce n'est pas une supposition, c'est une conséquence de F=mdv/dt avec v(t=0)=0.
Vous pouvez le noter en début de question 3.