Diagramme de Bode

 Niveau licencePartager :
			        
Diagramme de Bode
Posté par 
macermite  10-04-12 à 00:00
Bonsoir,

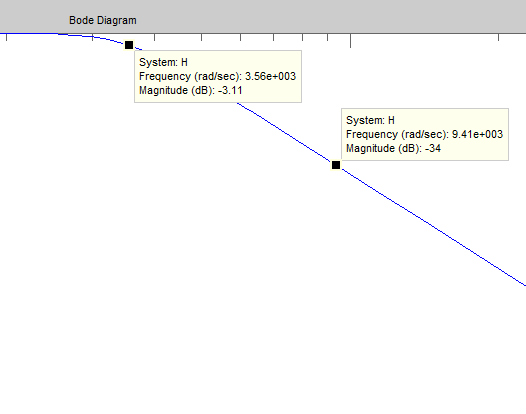
Je cherche à calculer l'ordre d'un filtre dont je joins une partie du diagramme de bode. Je pars sur le fait que N*(-20 dB/décade) me permettra de connaître l'ordre N. Mais voilà je trouve une valeur de N trop importante. Pouvez-vous m'aider ?

Merci.

Edit Coll : images placées sur le serveur de l'  Merci d'en faire autant la prochaine fois !      
 Posté par 
macermitere : Diagramme de Bode  10-04-12 à 00:05
Avec cette image , c'est plus lisible

Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !      
 Posté par 
sanantonio312re : Diagramme de Bode  10-04-12 à 09:09
Bonjour,

Le premier point que tu as choisi n'est pas vraiment sur la partie droite.

Et le rapport entre les fréquences n'est ni 2 ni 10 pour utiliser le -6dB/octave ou -20/décade.

Néanmoins, si on considère les deux points sur le droite: 

GdB-34+3.11=-30.89 dB

9.41/3.562.64

-30.892/2.64-23.4-46

Ce qui militerait pour un ordre 4.
 Posté par 
J-Pre : Diagramme de Bode  10-04-12 à 10:30

Le diagramme asymptotique du gain dégringole à 80 db par décade.

---> ordre 4.

 Posté par 
macermitere : Diagramme de Bode  16-04-12 à 14:10
Bonjour,

pourrais-tu détailler tes calculs ? je ne comprends pas le raisonnement.
 Posté par 
J-Pre : Diagramme de Bode  16-04-12 à 15:25
Si c'est de ma réponse que tu parles ... Je n'ai fait aucun calcul.

Je me suis contenté de mesurer, sur le graphique, la pente de l'asymptote.

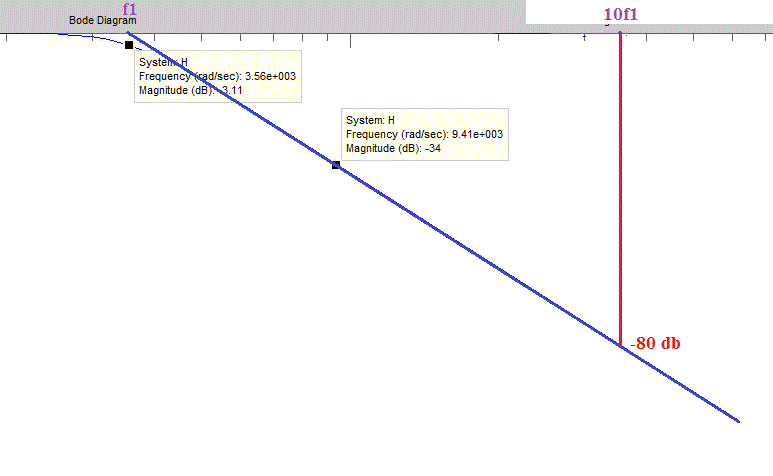
Sur une décade (En passant de f1 à 10f1 ou plutôt en passant de w1 à 10 w1), l'asymptote passe de 0 db à -80 db.

Facilement mesurable puisque on connait l'échelle utilisée pour les dB par le point en w = 9410 rad/s (-34 dB) et que l'axe des w est gradué (je l'ai juste prolongé en respectant la graduation logarithmique).

On mesure donc sur le graphe, une pente de 80 db par décade pour le diagramme asymptotique ...

Et cela correspond alors à filtre d'ordre 4.

 Posté par 
macermitere : Diagramme de Bode  16-04-12 à 15:51
oui, je connais la méthode graphique. Mais si je ne dispose pas de graphique mais de valeurs numériques uniquement je suis obligé de faire des calculs du genre à sanantonio312.

et là cela se complique ...
 Posté par 
J-Pre : Diagramme de Bode  16-04-12 à 17:37
Et si tu donnais l'énoncé dont tu disposes vraiment.

Tu dis que tu n'as pas de diagramme ... mais tu en dessines un.

 Posté par 
macermitere : Diagramme de Bode  16-04-12 à 18:02
Il ne s'agit pas d'un exercice, mais une application pratique que je me suis donné. Sachant lire le graphique comme tu l'as exposé je me suis posé la question de savoir si il existait une méthode "calculatoire" pour retrouver le même résultat.
  Posté par 
sanantonio312re : Diagramme de Bode  16-04-12 à 18:59
Bonjour, 

J'ai juste fait une règle de 3 entre tes deux fréquences dont le rapport est d'environ 2.64 pour le ramener à 2: une octave.

J'ai ensuite divisé la différence de gain ramenée à une octave par 6 (-6dB/octave) pour avoir une approximation de l'ordre.

Mais avec le premier point qui n'est visiblement pas sur l'asymptote, c'est assez approximatif.