Inscription / Connexion Nouveau Sujet
Déterminer fonction transfert
Bonsoir, je bloque sur une question qui devrait être assez simple j'aurai besoin de votre aide !
Enoncé :
La source de tension a pour f.e.m : e(t)=E*cos(
t)
[
pour notations complexes]
J'ai donc fais 1 Loi des Noeuds et 2 Lois des Mailles en notation complexe mais je n'arrive pas à éliminer les I, I1 et I2 pour trouver la fonction de transfert H=(Us)/(E) qui doit être égale à H=1/[1+(j/Q)(x-1/x)] avec x=/0 , 0=1/sqrt(L*C) et Q=(L*0)/R=1/(RC0)
Voici le montage électrique :
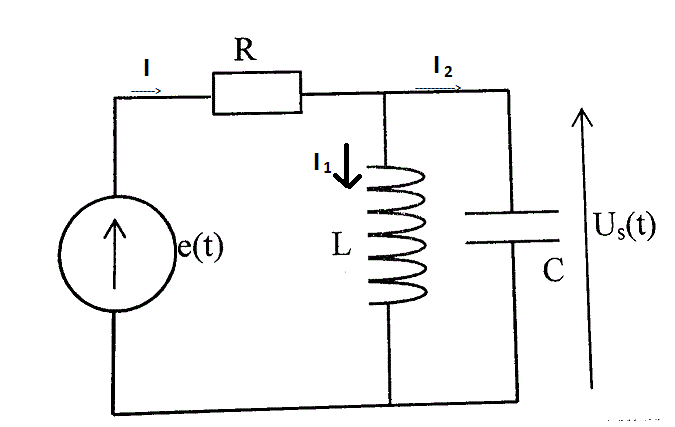
Bonsoir.
Ce n'est pas comme ça qu'on procède.
Il faut raisonner avec l'impédance équivalente entre L et C et appliquer le pont diviseur de tension.
C'est tellement plus rapide...
Z = (jwL/(jwC))/(jwL + 1/(jwC))
Z = jwL/(1-w²LC)
Us/Z = e/(R + Z)
Us/e = Z/(R+Z)
Us/e = [jwL/(1-w²LC)]/[R + jwL/(1-w²LC)]
us/e = jwL/[R(1-w²LC) + jwL]
us/e = 1/[1 - j.R(1-w²LC)/(wL)]
us/e = 1/[1 - j.RC(1-w²LC)/(wLC)]
en posant wo²= 1/(LC) --->
us/e = 1/[1 - j.RC(1 - w²/wo²)/(w/wo²)]
us/e = 1/[1 - j.RC(wo² - w²)/w]
us/e = 1/[1 - j.wo.RC(wo² - w²)/(w.wo)]
us/e = 1/[1 - j.wo.RC(wo/w - w/wo)]
us/e = 1/[1 + j.wo.RC(w/wo - wo/w)]
et en posant Q = 1/(wo.RC) et x = w/wo
Us/e = 1/[1 + (j/Q).(x - 1/x)]
-----
Sauf distraction. 
Annuler
connectez vous