Inscription / Connexion Nouveau Sujet
Détermination du nombre d'étage
Bonsoir tout le monde, je suis bloqué, j'ai besoin d'aide s'il vous plaît. Et j'aimerai que vous m'aider à vérifier mon équation si c'est correcte.
Exo:
Un immeuble comporte N étage. Madame X à la fenêtre du 3éme étage voit passer un pot de fleur provenant d?un étage supérieur à la hauteur de sa fenêtre h = 1,30 m et la durée de passage du pot de fleur est de 0,10 seconde.
De quel étage le pot de fleur est-il tombé sachant qu?entre deux appuis de fenêtre consécutifs la distance H = 2,75 m.
Mon raisonnement :
Soient H, h et N les hauteurs respectives entre deux appuis, hauteur d'un étage et nombre d'étage.
Donc, Nh=nombre total d'étage de l'immeuble,
Pour le premier étage N=1, h
hauteur du 3éme étage N=3h
La hauteur entre à partir du 3ème étage et l'étage supérieur est H'=Nh-3h.
H'=(N-3)h; N-3=H'/h==>N=(H'/h)+3
Je suis bloqué ici,
De l'aide svp.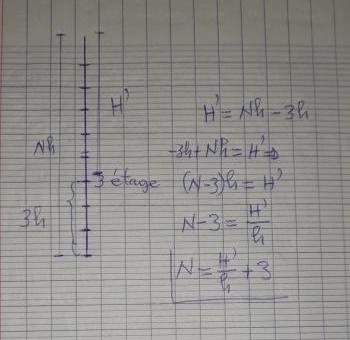
**image tournée et recadrée**rafraîchir la page**
Bonjour
On peut commencer par exprimer la distance parcourue quand le pot apparaît en haut de la fenêtre du 3ème étage :
Cette distance est H si le lancement s'effectue du quatrième étage ;
Cette distance est (2H+h) si le lancement s'effectue du 5ième étage ;
Cette distance est (3H+2h) si le lancement s'effectue du 6ième étage ;
Si n est le numéro de l'étage de lancement, le pot apparaît en haut de la fenêtre du troisième étage après avoir parcourue la distance :
x=(n-3)H+(n-4)h
tu peux ensuite calculer la distance (x+
x) parcourue quand le pot disparaît au regard en arrivant en bas de la fenêtre du troisième étable.
Je te laisse continuer...
Me
Bonjour
On peut commencer par exprimer la distance parcourue quand le pot apparaît en haut de la fenêtre du 3ème étage :
Cette distance est H si le lancement s'effectue du quatrième étage ;
Cette distance est (2H+h) si le lancement s'effectue du 5ième étage ;
Cette distance est (3H+2h) si le lancement s'effectue du 6ième étage ;
Si n est le numéro de l'étage de lancement, le pot apparaît en haut de la fenêtre du troisième étage après avoir parcourue la distance :
x=(n-3)H+(n-4)h
tu peux ensuite calculer la distance (x+
x) parcourue quand le pot disparaît au regard en arrivant en bas de la fenêtre du troisième étable.
Je te laisse continuer...
Merci Vanoise pour votre réponse, je me demande où allons nous utiliser le temps de passage du pot de fleur à 3éme étage
Je suppose le pot abandonné sans vitesse initiale au bas de la fenêtre du nième étage à la date t=0. En négligeant les frottements :
x=(n-3)H+(n-4)h=½gt2
x+x=(n-3)H+(n-3)h=½g(t+t)2
avec t=0,1s
Cela donne un système à deux inconnues...
Je suppose le pot abandonné sans vitesse initiale au bas de la fenêtre du nième étage à la date t=0. En négligeant les frottements :
x=(n-3)H+(n-4)h=½gt2
x+
x=(n-3)H+(n-3)h=½g(t+t)2
avec
t=0,1s
Cela donne un système à deux inconnues...
Ok merci beaucoup, je vais tenter et je vous reviendrai.
Réflexion faite, je crois que j'ai mal interprété la signification de H et la notion d'appuis consécutifs. Si h désigne la hauteur d'une fenêtre, H désigne la hauteur d'un étage tout simplement. Je reprends donc mon raisonnement.
La hauteur entre l'appui d'une fenêtre et le haut de la fenêtre juste en dessous est ainsi (H-h)
Si n=4 : la hauteur de chute pour arriver en haut de la fenêtre du troisième étage est (H-h)
Si n=5 : la hauteur de chute pour arriver en haut de la fenêtre du troisième étage est H+(H-h)
Et ainsi de suite. Si n est le numéro de l'étage de lancement, le pot apparaît en haut de la fenêtre du troisième étage après avoir parcouru la distance :
x=(n-3).H-h
Il arrive donc en bas de la fenêtre du troisième étage après avoir parcouru la distance (n-3).H
On obtient finalement le système de deux équations :
(n-3).H-h=½gt2
(n-3).H=½g(t+t)2
Annuler
connectez vous