Inscription / Connexion Nouveau Sujet
Détermination de la vitesse
Bonjour,
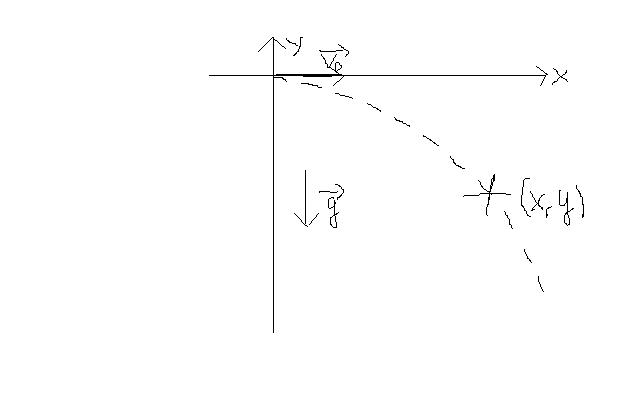
Voici mon énoncé : On étudie l'écoulement d'un jet d'eau sortant d'une gouttière dont la trajectoire décrit une parabole. On est dans un cas de chute libre. On peut schématiser ce jet comme dans l'image ci-dessous.
J'ai une égalité me donnant l'expression de la vitesse à partir des données :
, où x est l'abscisse du point du jet, y son ordonnée, et g le champ de pesanteur.
Comment prouver que la vitesse a effectivement cette expression ?
Je bloque, merci pour l'aide que vous pouvez m'apporter. Je suppose simplement que le vecteur vitesse est la dérivée du vecteur position par rapport au temps, mais je ne sais en déduire l'expression pour autant.
Sur le fichier, on ne voit pas bien, mais il s'agit de v0 pour le vecteur parallèle à l'axe des abscisse.
Merci d'avance de votre aide
La seule force agissant sur une masse m d'eau est son poids P = mg (vertical vers le bas)
On a donc F = m.g vertical vers le bas
---> d²y/dt² = -g
dy/dt = -gt + K et la composante verticale de la vitesse est nulle en t = 0 ---> K = 0
dy/dt = -gt
y(t) = -gt²/2 + K1
Et avec le repère choisi, y(0) = 0 ---> K1 = 0
y(t) = -gt²/2
En négligeant les frottements de l'eau dans l'air, on a : Composante horizontale de la vitesse = Vo et donc x(t) = Vo.t
On élimine t entre y(t) = -gt²/2 et x(t) = Vo.t
y = -g/2 * x²/Vo²
Vo² = -gx²/(2y)
Vo = Racinecarrée(-gx²/(2y))
-----
Sauf distraction. 
On a donc F = m.g vertical vers le bas
---> d²y/dt² = -g[quote]
Merci; mais à quoi est due cette égalité ?
Il y a un minimum de connaissances en physique à avoir pour pouvoir mettre un problème en équation.
La seule force agissant sur l'eau est le poids de l'eau, celle force est verticale dirigée vers le bas.
L'eau subit donc une accélération verticale vers le bas égale à l'accélération due à la pesanteur (g)
L'accélération verticale est par définition égale à d²y/dt² (mais son sens positif est vers le haut si l'axe des y du repère est dirigé vers le haut).
Donc, avec le repère du dessin, on a : d²y/dt² = -g



