Inscription / Connexion Nouveau Sujet
Détente adiabatique d'un gaz parfait
Bonjour,
Voici l'énoncé d'un exercice de thermodynamique qui me paraissait simple au premier abord mais qui finalement me donne du fil à retordre :
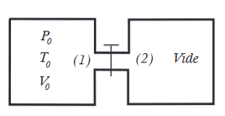
Il y a deux réservoirs (1) et (2) cotes à cotes, reliés par un robinet.
Les deux réservoirs ont le même volume et l'ensemble est adiabatique. On entrouvre le robinet : le gaz parfait restant dans le compartiment (1) a subit une transformation quasi-statique.
Déterminer l'état final et décrire le chemin suivi pendant la transformation, dans le cas où les réservoirs sont thermiquement isolés l'un de l'autre (ce qui revient à négliger le transfert thermique entre les gaz se trouvant dans (1) et (2) à l'état final).
La correction donne :
A vrai dire, je ne sais pas vraiment comment trouver ce résultat, mais voici mes pistes :
La transformation est adiabatique, donc
Transformation quasi-statique signifie réversibilité.
La loi de Laplace-Poisson peut donc être utilisée (adiabaticité + réversibilité + gaz parfait) :
Enfin, la loi des gaz parfaits :
Pourriez-vous m'indiquer une piste de résolution ou m'aiguiller ? Je ne demande pas la réponse mais simplement une aide pour réussir cet exercice.
Bonjour
Il s'agit d'une détente adiabatique dans le vide puisque le réservoir n° 2 est initialement vide.
Q=0 donc
Que vaut W ?
Attention : noter  Q plutôt que Q est une véritable horreur ! Il faut bien faire la différence entre variation et quantité. J'ai eu l'occasion de rappeler cela sur cette fiche, à la fin du paragraphe 2.
Q plutôt que Q est une véritable horreur ! Il faut bien faire la différence entre variation et quantité. J'ai eu l'occasion de rappeler cela sur cette fiche, à la fin du paragraphe 2.
![]() Premier principe de la thermodynamique
Premier principe de la thermodynamique
Etant donné que le réservoir n°2 est vide, il n'y a pas de force de pression et donc ?
Et donc la variation d'énergie interne est nulle ?
Effectivement, mais je ne trouvais pas la lettre (pour
).
Effectivement : cela revient à dire que l'énergie interne du gaz dans l'état initial est égal à la somme des énergies internes des gaz dans les deux récipients à l'état final.
A vrai dire, je ne sais pas trop quoi en tirer.
D'après la 1ère loi de Joule : . Alors si la variation d'énergie interne est nulle, la température est constante tout au long de la détente.
Mais étant donné que l'on a du en puissance, je pensais utiliser la loi de Laplace-Poisson pour commencer, mais je n'ai pas trop de pistes. Voici mes quelques résultats :
et
et
, alors
Mais lorsque je remplace : , je trouve un résultat qui est incohérent.
Pourriez-vous m'aiguiller sur la piste de départ ?
A vrai dire, j'aurais dit que non, car la transformation me semble irréversible.
Mais dans l'énoncé, il est évoqué une transformation quasi-statique. Et je ne vois pas d'autre moyen d'obtenir un terme avec une puissance.
Je peux te résumer les différentes étapes. Il faut supposer que, à l'équilibre final, P1=P2, V1=V2 =Vo mais T1 T2 : les gaz sont à l'état d'équilibre mécanique mais pas à l'état d'équilibre thermique à l'état final.
T2 : les gaz sont à l'état d'équilibre mécanique mais pas à l'état d'équilibre thermique à l'état final.
1° : Écrire comme déjà dit :  U1+
U1+ U2=0
U2=0
Cela va te donner une relation entre n1, T1, n2, T2, To.
2° : Appliquer la loi des gaz parfaits à chacun des gaz des deux réservoirs à l'équilibre final va te permettre, en tenant compte de la relation précédente d'obtenir une expression très simple de P1=P2 en fonction de Po.
3° : Il faut supposer la détente du gaz présent dans le récipient 1 suffisamment lente pour être qualifiée de quasi statique... C'est une assez grosse approximation bien sûr mais elle permet d'aboutir au résultat de ton corrigé.
Je dois donc me servir des expressions suivantes pour arriver au résultat ? :
Soit ? Alors
Aussi, ,
car
,
Il n'y a que pour l'expression du 1er principe, avec la somme des énergies internes nulles, que je ne vois pas trop quelle relation en tirer ?
Étape n° 1 : Je suppose a priori qu'à l'état final, les deux réservoir ne contiennent pas les mêmes quantités de gaz que je note n1 et n2 avec évidemment n1+n2=no (quantité initiale dans le réservoir de gauche sur le schéma). En notant Cvm la capacité thermique molaire isochore du gaz :
n1.Cvm.(T1-To)+n2.Cvm.(T2-To)=0
Soit :
n1.T1+n2.T2=no.To (relation 1)
Étape n° 2 : en appliquant 3 fois l'équation d'état : une fois à l'état initial puis à l'état final aux gaz présents dans les deux réservoirs, sans oublier l'équilibre mécanique final : P1=P2, je te laisse démontrer la relation simple existant entre P1=P2 et la pression initiale Po.
Étape n° 3 : en supposant la détente suffisamment lente, on peut appliquer la loi de Laplace aux n1 moles de gaz entre l'état initial et l'état final. Attention : la loi de Laplace ne s'applique qu'à un système fermé (quantité fixe de gaz) : il ne faut donc l'appliquer qu'aux n1 moles de gaz, pas à la totalité du gaz...
La correction donne :
Peux-être une erreur de copie de ta part. En tout cas, ce résultat est nécessairement faux car il n'est pas homogène. Il est assez facile d'exprimer n1 puis n2 en fonction de no et de
Bonjour,
En suivant les indications de Vanoise, on a : P1 = Po/2 =P2
Si on applique la loi de Laplace (détente adiabatique) aux n1 moles de gaz :
-initialement ces n1 moles occupent - il me semble ? - le volume Vo*n1/(n1+n2) ; à la pression Po : c'est juste ?
-au final elles occupent le volume Vo ; à la pression Po/2 ;
Je trouve la relation : n1/n2 = 1/[2^^(1/gamma) -1]
Estce juste ?
Bonsoir Chimival
Tout calcul fait, je pense que l'auteur du corrigé de cet exercice a voulu écrire :
où n est la quantité totale de gaz, ce que j'ai noté no dans mon message précédent.
Cela dit, ton raisonnement et tes résultats sont corrects. Francois255 a laissé tombé. J'imagine que la suite de l'exercice consiste à exprimer les températures T1 et T2 dans les deux réservoirs. Il serait aussi intéressant d'exprimer la variation d'entropie du gaz et de commenter physiquement le signe du résultat.
Cela dit : il s'agit ici d'un bon exercice ”théorique” permettant aux étudiants de se familiariser avec les lois de la thermodynamique. En pratique, je ne vois pas trop comment expérimentalement, il est possible d'obtenir un transfert de matière d'un réservoir à l'autre tout en empêchant les transferts thermiques par convection. Expérimentalement, la détente dans le vide conduit très rapidement à un équilibre mécanique comme expliqué ici : P1=P2 mais aussi, au bout d'un temps assez court, à un équilibre thermique : T1=T2. Cela ramène à l'étude classique de la détente de Joule et Gay-Lussac...
Bonjour Vanoise,
Merci pour la réponse et ces explications !
- Pour T1, on a T1 = To*2^^(1/gamma -1) ; comme gamma >1, T1 décroît de To à To/2 ; il me semble que c'est logique (détente adiabatique) ;
- Pour T2, on a T2 = To/2[ 1-2^^(-1/gamma)] ; on voit que T2 croît de T0 à l'infini selon la valeur de gamma ;
-Pour la variation d'entropie, je dirais que Delta S = Delta S1 + Delta S2 ; il me semble que la variation d'entropie des n1 moles de gaz, Delta S1 =0 car la transformation est adiabatique quasi-statique, non ?
-Pour la variation d'entropie des n2 autres moles, Delta S2 = n2*R*[1/(gamma-1) Log (T2/To) + Log (n/n1)] ; elle est toujours >0 car irréversible
Bonjour,
Veuillez me pardonner pour l'absence de réponse, je pensais avoir trouvé la solution en fin de semaine dernière mais je me suis rendu compte qu'il y avait une erreur dans mon raisonnement, alors je cherchais de mon coté. Mais je n'ai pas laissé tombé, loin de la.
La relation toute bête qui me manquait était effectivement , et non pas
comme je partais au départ.
Le résultat est effectivement , avec la puissance pour le terme 2 et non pas la quantité de matière.
Pour trouver le résultat néanmoins,je bloque toujours à un moment précis, et je ne trouve pas mon erreur, je ne comprend pas :** image supprimée **
L'image ne se met pas correctement dans le bon sens, désolé.
Je sais qu'il y a une erreur quelque part, mais impossible de la trouver !
--------------
***Tes pistes de réflexion doivent être recopiées***
Bonjour François255
A mon avis l'erreur est à l'état final :
on a : Pf.Vo/T1=Rn1 et Pf.Vo/T2 = Rn2 car les 2 réservoirs Vo ne sont pas à la même température !
Désolé de répondre tardivement mais je révise mes finaux et cet exercice est plus pour mon "loisir"...
Oui j'ai bien trouvé !
La transformation est adiabatique.
Il y a du vide de l'autre coté, les travaux des forces de pressions sont donc nuls
Alors d'après le 1er principe, .
D'après la 1ère loi de Joule pour un gaz parfait, . Avec
la masse molaire du gaz.
Après simplification :
Avec la loi des Gaz Parfaits :
Soit :
Or, les deux parties du gaz occupent le réservoir entier, c'est à dire un volume de valeur
Alors
D'où
D'accord avec ton raisonnement. Juste une remarque sur les notations.
Le symbole " " désigne une quantité élémentaire :
" désigne une quantité élémentaire :  Q,
Q,  W...
W...
Le symbole "d" désigne une variation élémentaire ; dU= Q+
Q+ W...
W...
Le symbole " " désigne une variation finie de paramètre d'état ou de fonction d'état :
" désigne une variation finie de paramètre d'état ou de fonction d'état :  U=W+Q...
U=W+Q...
D'accord merci, ici il faudrait plutôt utiliser alors.
Ensuite, dans l'énoncé, ce n'est pas écrit clairement, mais je le déduis connaissant le résultat, correspond à la quantité de matière du réservoir 1 ? C'est à dire que ces
moles de gaz occupent un volume
?
Sans la réponse, je ne sais pas si j'aurais trouvé cette information de moi-même, je pensais que représentait une quantité quelconque d'un volume quelconque. Mais il est plus bien plus logique après coup de considérer
comme la quantité de matière du réservoir 1. J'y penserai pour de futurs exercices.
Alors, la transformation étant quasi-statique, elle peut être considérée comme réversible. Le gaz est parfait. Les conditions pour utiliser la loi de Laplace-Poisson, appliquée aux moles, sont réunies :
A l'état initial, moles sont à pression
, à une température
et occupent un volume
.
A l'état final, cette même quantité de matière est soumis à une pression et occupent un volume
à une température
.
Or, à l'état initial, d'après la loi des gaz parfaits :
(totalité du gaz)
Soit : (cohérent car
donc
)
De plus, on a déjà prouvé que
Alors on obtient :
Après simplification :
Soit :



