Inscription / Connexion Nouveau Sujet
Descente en voiture
Bonjour à tous ! Voila le problème :
Une automobile de masse 1000kg descend , sans utiliser son moteur, une rue dont l'inclinaison a(alpha) est de 20°.
1) Donner les équations de la vitesse et position : J'ai trouvé v(t) = -gt + v0sin(alpha) et r(t)=-gt²/2 + (v0sin(a))t selon Uy et selon Ux j'ai 0.
2) Déterminer la force, supposée constante, produite par les freins si l'automobile se déplace avec :
a) un mvt uniforme ;
b) une accélération cte de a=0.2 m.s-2 ;
c) Trouver dans chacun des cas la force exercée sur l'automobile par la rue
Pour la 2 je ne trouve pas..
Je vous remercie !
1/
Tu donnes des équations ... sans avoir précisé le repère, c'est un manquement grave.
Choix du repère :
Avec le repère d'origine à la position de la voiture à l'instant t = 0.
Axe des abscisses suivant la ligne de plus grande pente de la rue, sens du haut vers le bas de la rue.
Accélération : dv/dt = g.sin(alpha)
v(t) = Vo + g.sin(alpha).t
dx/dt = Vo + g.sin(alpha).t
x(t) = Vo.t + g.sin(alpha)*t²/2
-----
2/
Résultante des forces sur la voiture hors freinage (et supposé sans autre frottement) : F = m.g.sin(alpha)
a) Si le mouvement est rectiligne uniforme, c'est que la force f de freinage est égale et opposée à F --> f = - m.g.sin(alpha)
b) si a = 0,2 m/s²
f = -(F - ma)
f = - (m.g.sin(alpha) - m.a)
f = - m*(g.sin(alpha) - a)
c)
N = mg*cos(alpha) (normale à la route, vers le haut)
-----
Sauf distraction. 
Je ne comprend pas bien le choix du repère. Il est à l'horizontal et passant par le point le plus haut de la pente ?
Merci beaucoup pour le reste !
Je ne comprend pas bien le choix du repère. Il est à l'horizontal et passant par le point le plus haut de la pente ?
Non.
C'est comme suit que je l'ai défini :
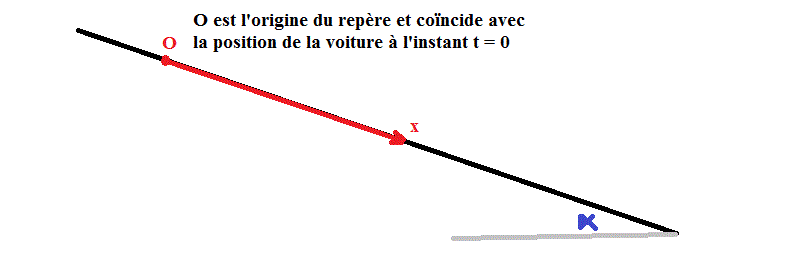
On peut évidemment définir un autre repère, mais dans le cas présent, c'est celui qui est le plus simple à utiliser.



