Inscription / Connexion Nouveau Sujet
Dérivées et approximations (diracs)
Bonjour !
Je fais appel à vous car je suis en train de réviser mes TDs sur l'analyse du signal numérique, et je bloque sur une chose.
Je vais donner l'exemple d'un des exercices qui est le suivant :
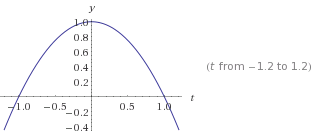
Calculer la transformée de Fourier de x(t) = 1 - t² si |t| < 1 ; x(t) = 0 sinon.
Vous trouverez plus bas une image (de Wolframalpha) qui illustre cette fonction.
Pour trouver cette transformée de Fourier, nous avons d'abord dans le TD calculé le maximum de dérivées de la fonction, on obtient:
x'(t) = -2t
x''(t) = -2
(Dans le cas où t est compris entre -1 et 1)
Et voici la dérivée 3ème (que l'on utilise pour calculer ensuite la transformée de Fourier):
Ce que je ne comprends pas, c'est comment on arrive à cette troisième dérivée.
J'ai bien compris que c'était une approximation, en cherchant sur internet j'ai trouvé différentes formules qui s'apparentaient un peu, comme celle des dérivées discrètes, ou des formules d'échantillonnage... J'ai testé différentes choses sans retrouver la bonne dérivée.
Voilà, je bloque sur ça alors que je suis sûr que c'est tout bête...
J'espère donc que quelqu'un pourra m'éclairer ! 
Merci d'avance.
Hello
1) pourquoi dériver successivement => pour arriver à une fonction dont tu connais la TF
car il ne reste plus ensuite qu'à appliquer la priorité de la transformation de Fourier
(tu dois avoir la TF d'un dirac retardé dans ton formulaire)
2) Pourquoi écrire
( car en fait x''(t) = 0 entre - et +
et +
 )
)
et bien simplement pour pouvoir retrouver la fonction x'(t):
C'est bon?
J'ai appuyé su "POSTER" au lieu de "Aperçu" 
Il faut bien sûr lire à la fin, avec le bon nombre de dérivations
( car en fait x'''(t) = 0 entre - et + )
et bien simplement pour pouvoir retrouver la fonction x'(t):
Je viens de me relire, c'est vraiment "patachon". Je reprends complètement par souci de clarté :
1) pourquoi dériver successivement x(t) => pour arriver à une fonction dont tu connais la TF.
car, une fois arrivé à une fonction dont on connait la TF, il ne reste plus ensuite qu'à appliquer la propriété de la transformation de Fourier
(tu dois avoir la TF d'un dirac retardé dans ton formulaire, certains formulaires incluent également la fonction "porte" ou "rectangle")
2) Pourquoi écrire la dérivée 3ème sous cette forme ... parce qu'il le faut:
( x''(t) = -2 devrait donner x'''(t) = 0 ?  )
)
Il faut pouvoir, en intégrant x'''(t) retrouver la fonction x''(t):
C'est bon cette fois?
PS: je ne vois pas à quoi le mot "approximation" fait référence dans le titre
Merci Dirac ! (Tu portes bien ton nom ^^)
Je pense que j'ai à peu près compris. 
Par contre j'ai une question, puisque la primitive de est la fonction Heaviside H(t), je ne comprends pas trop quelle valeur on prend pour H(0).
Parce qu'ici, dans le cas où t = 1, j'obtiens (à partir de l'expression de x''(t) que tu as indiqué dans ton post) :
Si je considère que H(0) vaut 0, j'obtiens bien -2, mais si je considère que H(0) = 1, j'obtiens 0. :/
Du coup je ne comprends pas bien comment fonctionne la fonction Heaviside en 0.
En espérant que tu puisses m'éclairer à ce sujet ! 
Hello
Juste pour m'assurer que tu ne te perds pas: pour résoudre cet exercice tu n'as pas pas besoin de chercher à "intégrer" les 2 intégrales introduites dans la définition de x'''. Tu dois (simplement) calculer la TF de x''' puis utiliser la propriété sur les TF de dérivées que je te proposais plus haut
Ceci étant dit, pour répondre à ta question
- la fonction de Heaviside n'est pas défini en 0. Donc écrire H(0)= 0 ou 1, ou 1/2 est "malhabile", je crois plus élégant d'écrire
On prolonge par continuité, x''(t) = 2 (Je te rappelle bien gentiment  que la discontinuité est imposée par x(t) et qu'il faut donc dès x' se donner les conditions qui permettront par intégration de bien retomber sur x(t) )
que la discontinuité est imposée par x(t) et qu'il faut donc dès x' se donner les conditions qui permettront par intégration de bien retomber sur x(t) )
ça te va mieux formulé ainsi? 
Merci pour ces explications 
Oui oui, je faisais le calcul des intégrales juste pour voir si je retombais bien sur x''(t). ^^
Mais en fait, je n'ai aucun problème à résoudre l'exercice, ma seule difficulté est de passer de l'expression de x''(t) à celle de x'''(t). 
Je me demandais s'il y avait une formule générale pour passer de l'une à l'autre, qui marche quelque soit la fonction.
C'est tout bête mais c'est juste ça qui me bloquait, je n'ai aucun mal à calculer la TdF, mais c'est juste exprimer une dérivée qui vaut 0 avec des diracs que je ne parvenais pas à faire.
Oui oui, je faisais le calcul des intégrales juste pour voir si ...
Ouf! j'étais inquiet

Cet exercice est un exercice d'application applicable aux signaux polynomiaux finis => méthode générale à retenir donc (peut être peux tu terminer l'exercice et rapporter tes résultats, nous devrions en voir émerger une autre)
OMG ça y est je viens seulement de comprendre la méthode en fait !! 
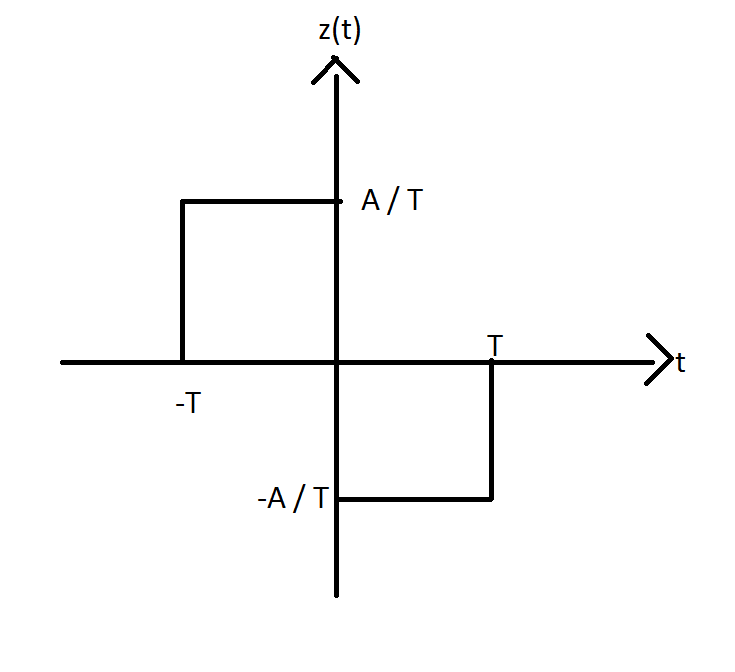
Il suffit de suivre la courbe, par exemple pour la fonction dont la courbe est en dessin ci-joint:
On commence à t = -T, comme on monte de A / T, on a
Ensuite à t = 0 on descend de 2 * A / T, on a donc
Et enfin, à t = +T, on remonte la courbe de A / T, on a donc
Ce qui finalement nous donne comme dérivée:
(C'est un de mes exercices corrigés, ce résultat est bon normalement.)
Voilà, donc j'ai passé du temps à me creuser la tête alors que la méthode était juste sous mes yeux, aïe aïe aïe... x)