Inscription / Connexion Nouveau Sujet
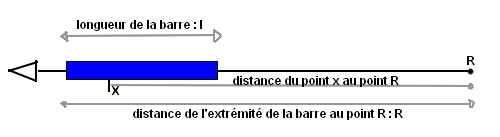
Densité de charge le long d'une barre
Bonjour !
Je (re)découvre l'électricité (et les intégrales aussi d'ailleurs) après une petite année d'inactivité. J'essayais donc de me rafraîchir la mémoire jusqu'à ce que je tombe sur un exercice assez compliqué ... pour moi du moins 
Voici la démonstration :
Donc là, le "r" représente la distance du point x au point R.
Ensuite on passe à ça ! Je sais que dq=Lamda*L, mais pourquoi "r" alors ? Ca n'a pas de sens je trouve ...
Là c'est pire, on intègre comme si la variable au dénominateur et numérateur était la meme !
Une petite explication s'il vous plait ? Je suis censé connaitre ça pour demain, histoire de ne pas être trop retardé par rapport aux autres 
bonsoir,
la formule dq =  dl est une formule générale
dl est une formule générale
ça ne veut pas dire que l'élement de longueur sera tjs noté dl
ça peut très bien être dx, dr, ds,... en fonction du paramétrage de la courbe qu'on définit
d'autre part -1/r est bien une primitive de 1/r2
Mais le "dr" du numérateur n'est pas le meme que celui du dénominateur ! Enfin on ne parle pas de la meme chose, non ?
Le "dr" au numérateur vient de dq=lamda*dr, donc c'est la longueur de la barre.
Alors que le "r" au numérateur est la distance qui sépare le point x du point R.
Dooonc pour être correcte on aurait du faire l'intégrale de 1/r^(2) en fonction de dl ! Et la variable "l" n'existe pas dans l'intégrale ...
Non ?
ok, je vois.
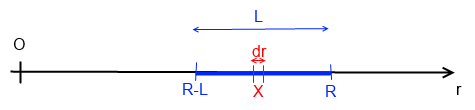
ici dl = dr puisque la droite (XR) et le fil rectiligne (la barre) sont confondus.
c'est le même axe où les points sont repérés par la coordonnée r et où l'élément de longueur vaut donc dr
dans la formule générale dq =  dl
dl
dl représente un élément de longueur infinitésimal du fil
ici le fil est rectiligne et est apparemment défini sur un axe (O,r) (cf dessin) donc l'élément de longueur est dr par définition
dl n'a pas de sens dans cet exo.
ici le dl de la formule générale se note dr
et dans une autre situation ce sera ds ou dx (tout dépend de la façon de paramétrer la courbe formée par le fil)
Désolé mais je ne comprend toujours pas 
Q = Lambda * L où Q est la charge pour une longueur L.
dQ = Lambda * dl où dQ est la charge pour une longueur dl.
Donc une tige de longueur L peut être divisé en plusieurs petite partie dl qui ont une charge élémentaire dQ.
Si r est la distance (grande) qui sépare une charge élémentaire d'un point R, comment peut-t-on associé dr à dl si dl n'est qu'une petite partie de la TIGE ? Je ne comprends vraiment pas ! Et que représente dr ? Je suppose que c'est une petite partie de la distance qui sépare une charge élémentaire du point R ...
Enfin, c'est flou 
je ne sais pas comment te le dire: dl est une NOTATION très générale, ça représente l'élement de longueur infinitésimal (en X sur le dessin)
et ici ça correspond à dr avec le paramétrage retenu (cf mail précédent)
donc
dq =  dr
dr
et si tu intègre de R-L à R tu retrouves bien Q = Lambda * L
dans la formule du champ él. tu as deux choses totalement distinctes:
dq =  dl qui ici s'écrit
dl qui ici s'écrit  dr
dr
et la distance séparant R et X (avec tes notations)
ici il se trouve que cette distance vaut r puisque tu cherches le champ en R sur ton dessin (càd en O sur le mien) mais ça n'a rien à voir avec le calcul de dq
"c'est le même axe où les points sont repérés par la coordonnée r et où l'élément de longueur vaut donc dr"
Je pense avoir compris ! Lorsque vous dites l'élément de longueur c'est à dire la plus petite "unité" de longueur possible ? Et vu qu'ils sont parralèlle nous pouvons dire que dx=dr.
Enfin, parce qu'ils sont sur la même ligne ou parce qu'ils sont parallèle ?
Donc imaginons plusieurs droites parallèle, (a,b,c,d,...), on peut alors dire que da=db=dc=...
C'est bien ça ?
Lorsque vous dites l'élément de longueur c'est à dire la plus petite "unité" de longueur possible ?
c'est plutôt l'élément infinitésimal de longueur (qu'on note par ex. dl dr dx ...)
ce n'est pas une unité de longueur puisque c'est arbitrairement petit
ici il n'y a qu'un axe (1 seule ligne, 1 seule dimension) donc une seule coordonnée (r)
donc pour calculer dq l'élément (infinitésimal) de longueur en X est dr
lis aussi mon mail précédent car nos mails se sont croisés je crois.
ici il n'y a qu'un axe (1 seule ligne, 1 seule dimension) donc une seule coordonnée (r)
donc pour calculer dq l'élément (infinitésimal) de longueur en X est dr
Si j'ai bien compris, l'élément infinitésimal est par rapport à un axe ? Donc l'élément infinitésimale d'un axe x sera égale à l'élément infinitésimal de toute droite parallèle à cette axe ?
pas vraiment; tu considères que le fil est la juxtaposition d'éléments de longueur infinitésimale notée dl
et dl s'exprime en fonction de la géométrie du problème et du paramétrage de la courbe.
ici le fil est rectiligne et repéré sur un axe (O,r) sur mon dessin, donc dl c'est dr
si on avait appelé l'axe (O,x) dl deviendrait dx
si le fil était un cercle on aurait dl = R d en paramétrant le cercle en polaires (r,
en paramétrant le cercle en polaires (r, )
)
si la forme était quelconque on prendrait dl = ds (abscisse curviligne)
etc.