Inscription / Connexion Nouveau Sujet
Déménagement !
Dans cet exercice, j'ai quelques difficultés.
Soit un réfrigérateur assimilé à un objet ponctuel de masse m. On souhaite déplacer celui-ci du rez-de-chaussée au 1er étage. Pour cela deux méthodes sont généralement employées :
1) Tirer le réfrigérateur verticalement avec une corde depuis le 1er étage.
(a) Représenter sur le schéma les forces appliquées au réfrigérateur. j'ai réussi
(b) Calculer la force nécéssaire pour le porter. (je pense que c'est : mg)
Dynamique frottements : Déménagement
2) Faire glisser le réfrigérateur dans les escaliers.
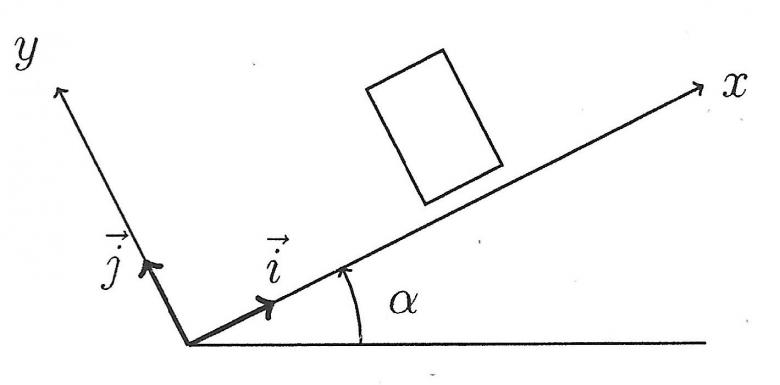
(a) Les escaliers, assimilés à une rampe lisse, faisant un angle \alpha avec le sol et en négligeant les forces de frottements, représenter sur le schéma les forces appliquées au réfrigérateur : son poids \vec{P}, la force de traction \vec{T}, et la réaction du sol \vec{N}.
J'ai réussi
(b) Exprimer les composantes de ces forces dans la base (\vec{i}, \vec{j}).
Px=-mg sin alpha
Py=-mgcosalpha
Tx=T
Ty=0
Nx=0
Ny=N
(c) En appliquant le principe fondamental de la dynamique selon l'axe \vec{i}, calculer la force de traction \vec{T} à appliquer au réfrigérateur pour le tirer à vitesse constante.
J'ai trouvé T=mg sin alpha
(d) Quelle méthode nécessite la plus grande force ?
Je pense que c'est la premier
(e) On considère désormais les forces de frottements appliquées au réfrigérateur. Le coefficient de frottement cinétique étant noté \mu _{c}, faire un nouveau schéma représentant les forces appliquées au réfrigérateur, et exprimer la force de frottement \vec{f} dans la base (\vec{i}, \vec{j}), sous la même forme qu'à la question 2. Puis, en appliquant le principe fondamental de la dynamique selon l'axe \vec{i}, calculer la force de traction nécessaire pour le tirer à vitesse constante.
je n'ai pas trouvé
Bonjour (sans s normalement😁
e) il faut appliquer les lois de Coulomb
En cas de glissement, la force de frottement f s 'oppose à la vitesse de glissement et on a: |f|= |N|
|N|
Ça doit figurer dans ton cours
Oui,tu as raison,
je vais rechercher un peu plus en détail,
mais mes autres reponses sont elles correctes ?
Merci et bonne journée
je n'arrive pas pour la suite, quelqu'un peut il me montrer comment partir ?
et me comfirmer mes réponses précedentes svp
Voici le shéma dans les escalier et j'ai donc trouvé
Px=-mg sin alpha
Py=-mgcosalpha
Tx=T
Ty=0
Nx=0
Ny=N
2e) sur le schéma suivant j'ai représenté la force de glissement f qui s'oppose a la vitesse , donc ici à T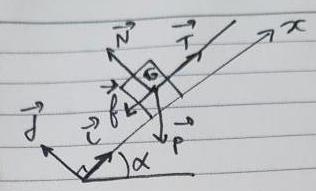
***Image recadrée***
oui ça j'avais réussi, merci de m'avoir confirmer , mais c'est poru calculer que je n'arrive pas
Merci

 ,
, ) ?
) ?

