Inscription / Connexion Nouveau Sujet
décomposition de vecteurs
Bonjour,
J'ai un exercice de mécanique à réaliser et j'ai un peu de mal. Est-ce que quelqu'un pourrait m'aider ou m'orienter?
Par avance merci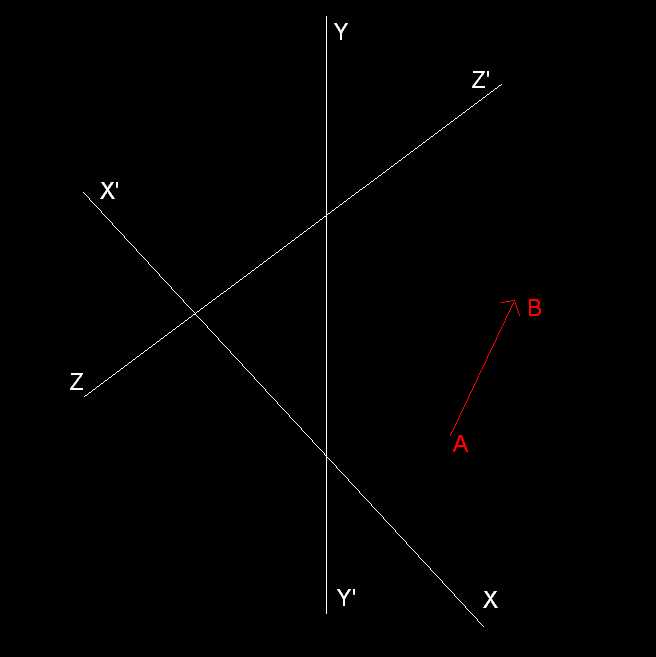
1) Dans un plan P on donne trois droites quelconques :X'X, Y'Y, Z'Z et un vecteur AB.
• Décomposer ce vecteur suivant les trois droites.
• Montrer que la décomposition n'est possible que d'une seule manière
Bonsoir bill447magnum,
cet exercice est du niveau de premiere et je m'etonne que tu aies des pb pour le resoudre. Je suis aussi surpris qu'il soit sur le forum de physique car c'est plutot un exercice de mathematiques.
La solution est pourtant simple : on projette orthogonalement les points A et B sur l'axe x'x, soit Ax et Bx ; on fait de meme sur l'axe y'y, soit Ay et By ; et aussi sur l'axe z'z, soit Az et Bz. On peut alors ecrire =
+
+
(appliquer la relation de Chasles a des vecteurs identiques a
,
et a
).
Si on prend des vecteurs unitaires  ,
,  et
et  respectivement sur x'x, y'y et z'z, on pourra ecrire
respectivement sur x'x, y'y et z'z, on pourra ecrire = AxBx
 + AyBy
+ AyBy + AzBz
+ AzBz .
.
Comme les six points Ax, Ay, Az, Bx, By et Bz sont uniques, la decomposition de est unique.
Prbebo.
J'ai pensé à faire cette démarche aussi mais mon professeur m'a donné cette méthode que je ne saisis pas, tel que:
"Tracez le point C intersection de AB avec l'un des axes. Puis D le point d'intersection
des deux autres axes. Il suffit de commencer par décomposer AB sur CD et le premier
axe …..(pensez à faire glisser vos vecteurs sur leur supports)"
Bonjour à tou(te)s,
Désolé de déterrer ce vieux sujet mais je suis confronté au même exercice et ne trouve pas de solution, j'aurais tendance à projetter orthogonalement le vecteur sur les trois axes mais mais pour quel résultat ??
Quid du dernier post de "bill447magnum" ?? Si quelqu'un peut me mettre sur la voie je vous en serais très reconnaissant.
Merci
bonjour ugolin83,
un an et demi après la mise en ligne de cet exercice, ma position reste la même :
1 - c'est un exercice de mathématiques et non de physique ;
2 - il est du niveau de première (plutôt terminale maintenant, bien que la relation de Chasles figure au programme du DNB) ;
3 - c'est surtout un exercice stupide (ou alors il y a une subtilité qui m'échappe), car puisque la projection orthogonale d'un point sur une droite (on dit maintenant "le projeté") est unique, celle d'un vecteur (= 2 points) l'est aussi. Le vecteur vec{AB} ayant alors une projection unique sur chaque droite, appelées respectivement vec{AxBx}, vec{AyBy} et vec{AzBz} dans ma réponse, l'écriture vec{AB} = vec{AxBx} + vec{AyBy} + vec{AzBz} est nécessairement unique.
La "méthode" proposée par le professeur de Magnum ne sert à rien, sinon à remplacer une solution simple par un raisonnement compliqué.
Juste une remarque : si les trois droites sont coplanaires (l'énoncé ne dit rien à ce sujet), deux projections suffisent pour écrire vec{AB}. Si non, il faut garder les trois.
Bon courage pour la suite.
Prbebo.
Bonjour et merci prbebo,
J'ai effectivement lu les remarques faites il y'a maintenant longtemps...
L'énoncé complet est :
Dans un plan P on donne trois droites quelconques : x'x y'y z'z et un vecteur AB
1 - Décomposer ce vecteur suivant les trois droites.
2 - Montrer que la décomposition n'est possible que d'une seule manière
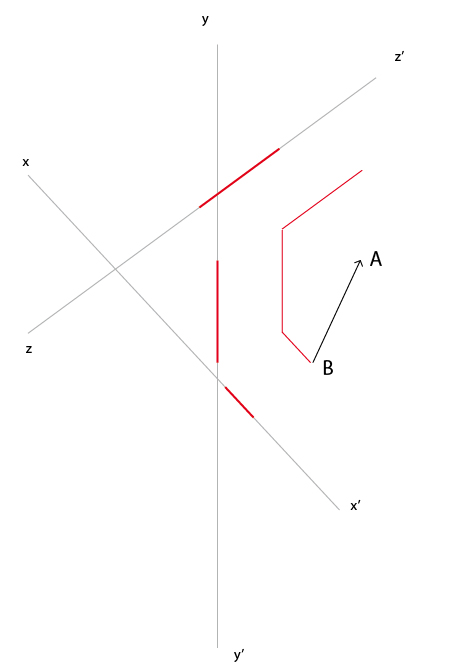
Visiblement si l'on parle d'un plan P c'est que les 3 droites sont dans celui-ci ?? Sauf que graphiquement, la somme des trois projetés n'est pas égale à vectAB... (voir pièce jointe). Est-ce justement la réponse au 2) -> pour que ce soit possible il faut que l'un des axes ne soit pas dans le plan P ??
Sinon, de prime abord je dirais :
1) la décomposition coule de source, on projette orthogonalement le vecteur sur les 3 axes.
2) par exemple, pour que la décomposition soit possible il faut que x'x, y'y et zz' soit dans le même sens (positif ou négatif mais dans le même sens...) ??
J'avoue ne pas trop comprendre l'intérêt de cet exercice... sur le forum de math(où le même exercice a été soumis), certains disent :
"il y a une erreur dans l'énoncé, il n'y aura jamais unicité de la décomposition d'un vecteur dans une famille qui n'est pas libre"
Euh, je ne comprend pas trop cette phrase...
En tous cas merci encore.
Bonjour,
L'île des sciences physiques est réservée aux problèmes et exercices de physique et de chimie…
Tu es invité(e) à changer d'île et à te rendre sur l'île des mathématiques :  Ile des mathématiques
Ile des mathématiques


