Inscription / Connexion Nouveau Sujet
decharge d'un condensateur
bonjour
j'ai un exercice a faire j'aimerai réussir a comprendre parce que j'ai vraiment du mal avec ce chapitre d'électricité
merciii en avance
ennocé:
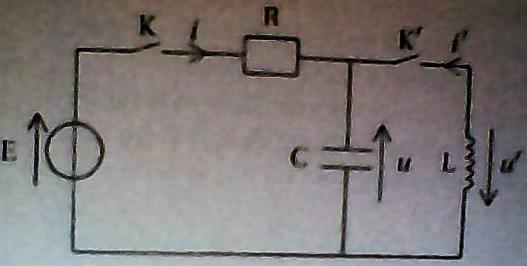
On s'intéresse dans un premier temps à la décharge d'un condensateur à travers une bobine idéale et on considère le circuit suivant :
(pièce jointe)
lorsque le régime est établi id est lorsque le condensateur de capacité C est chargé, on ouvre l'interrupteur K initialement fermé et on ferme l'interrupteur K' initialement ouvert. L'instant correspondant est pris comme nouvelle origine des temps. Les données sont I ,C et E .
1/ déterminer la tension initiale du condensateur avant le basculement de K' .
2/ établir l'équation différentielle vérifiée par la tension u en fonction du temps
3/ déterminer l'expression de la tension u en fonction du temps.
4/ en réalité, on observe des oscillations pseudo-périodique . L'amortissement constaté est du à la résistance interne r de la bobine . Les données sont maintenant r, L, C et E
comment peut-on visualiser la tension u en fonction du temps dans le cas du régime pseudo-périodique observé.
5/ établir l'équation différentielle vérifiée par la tension u aux bornes du condensateur .
6/ déterminer l'expression de la tension u en fonction du temps dans le cas du régime pseudo-periodique observé .
7/sachant que L=10mH, C=1,0 microF et E=6,0V, déterminer la valeur numérique de la pulsation propre w0 du circuit dans le cas d'une bobine idéale (sans résistance interne r).
8/la pseudo-periodique mesurée est T=0,63ms . Calculer la pseudo-pulsation omega et en déduire la valeur numérique de la résistance r de la bobine réelle.
9/ donne l'allure de la courbe représentative de la tension aux bornes du condensateur dans le cas d'une résistance r de valeur élevée.
Pour la premier question si j'ai bien compris faut mesurer la tentions on tenant compte que l'interrupteur K' ouvert e et K fermé .
J'ai pensé de faire deux fois la lois de mail vue qu on a deux nœud dans le circuit
premier loi de maille
E=iR
deuxième loi de maille
Uc= -U'L
Uc=-L*d^2Uc/dt
après est ce que j'ai le droit d 'additionné les deux loi de maille comme ca je me retrouve avec une équation différentielle de deuxième ordre ? Est ce déjà je déboute bien ou j'ai des erreurs ?
J'aimerais bien comprendre et réussir a finir cette exercice
merci en avance
Salut,
Ton exercice est très proche d'une application de cours.
Je te transmets donc les deux fiches relatives à ce sujet :
Condensateurs et dipôles RC
Oscillations libres dans un circuit RLC
(notations à adapter à ton exercice)
merci beaucoup pour les fiches ca m'as bien aider pour la question 2 mais pour la question 1 la tension initiale du condensateur avant le basculement de K' c'est donc Uc ? ou faut determiner une valeur?
K' est ouvert, tu fermes K.
D'après la première fiche tu as un dipôle RC : le condensateur va se charger selon la solution de l'équation différentielle (cf. fiche) :
donc quand t tend vers l'infini, u(t) tend vers E.
oui je viens de comprendre merci beaucoup , mas de coup pour la question 3 quand ils disent de determiner l'expressio de la tension en fonction du temps c 'est la meme reponce que la question une c est a dire u(t) = E* (1 - e^(-1/RC) no?
Si je résume :
on suppose le condensateur initialement déchargé --> u(0) = 0 V
K' est ouvert
on ferme K
--> dipôle RC (cf. la fiche), on en revient à ce que je t'ai expliqué plus haut.
ensuite, dès que le condensateur est chargé :
on ouvre K
on ferme K'
--> dipôle rLC avec des pseudo-oscillations (cf. la deuxième fiche)
Annuler
connectez vous