Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Courant efficace utilisant Fresnel

Posté par
lachgar2 09-01-17 à 16:07

Bonjour à tous.

Une installation fonctionne sous une tension de valeur efficace U=220V et de fréquence f=50Hz.
Elle comporte en dérivation :
-un moteur M1 de puissance mécanique 3kW, de facteur de puissance cos1=0.70 et de rendement 1=0.75
-un moteur M2 de puissance mécanique 3kW, de facteur de puissance cos2=0.85 et de rendement 2=0.75
En adoptant la méthode vectorielle , on veut tracer la construction de Fresnel des différents courants pour déduire le courant efficace de l'installation.
Donc:  
Les valeurs efficaces des courants I1 et I2 ( en utilisant les puissances actives) :
I1=25.97 A
I2=21.39 A
1=45.57°
2=31.78°

On sait que :  Icos(wt+\phi )=I_{1}cos(wt+\phi _{1})+I_{2}cos(wt+\phi _{2})

Alors d?après la figure ci-dessous:

\large I²=\left[I_{2}+I_{1}cos(\phi _{1}-\phi _{2}) \right]²+I_{1}²sin²(\phi _{1}-\phi _{2})

Puis on fait le calcul pour trouver \large I=\sqrt{\left[I_{2}+I_{1}cos(\phi _{1}-\phi _{2}) \right]²+I_{1}²sin²(\phi _{1}-\phi _{2})}47 A

Et si l'on veut on peut déterminer   tel que  :

\large \tan \phi =\frac{I_{1}sin(\phi _{1}-\phi _{2})}{\left I_{2}+I_{1}cos(\phi _{1}-\phi _{2}) \right}=A \\ \\ \phi =\tan^{-1}(A)

Est ce que c'est correct?
Si oui,pourquoi j'ai pas trouvé le même résultat que quand je somme les deux courants I1 et I2?

Merci beaucoup.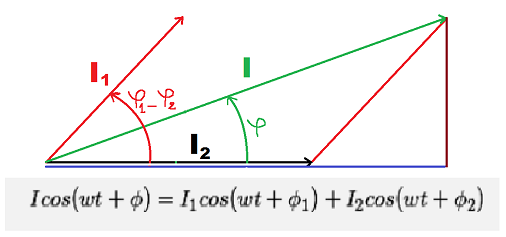

Courant efficace utilisant Fresnel

***Image recadrée***

Posté par
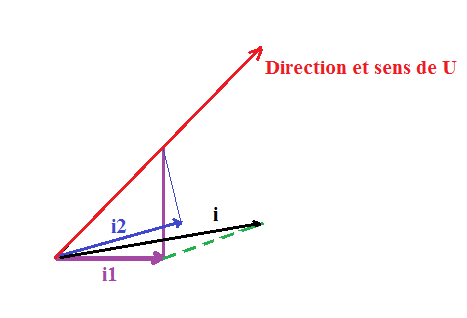
J-Pre : Courant efficace utilisant Fresnel 09-01-17 à 17:53

Courant efficace utilisant Fresnel

Si on met les 2 vecteurs i1 et i2 à la queue leu-leu, leur somme valant i, il forme un angle de 180° - (45,57° - 31,78°) = 166,21°

Al Kashi : i² = i1² + i2² - 2*i1*i2.cos(166,21°)

i² = 25,97² + 21,39² - 2 * 25,97 * 21,39 * cos(166,21°)

i² = 2210,946...

i = 47,02 A
-----

i1² = i² + i2² - 2*i*i2.cos(Phi)

25,97² = 47,02² + 21,39² - 2 * 47,02 * 21,39 * cos(Phi)

cos(Phi) = 0,991278...

Phi = 7,573 ° (entre i et i2)

Or entre i2 et U, on a Phi2 = 31,78°

--> angle entre U et i : 31,78 + 7,753 = 39,31°

Et donc pour l'installation : cos(Phi) = cos(39,31°) = 0,77
-----

Sauf distraction.  

Posté par
vanoisere : Courant efficace utilisant Fresnel 09-01-17 à 18:16

Bonsoir
Tu connais sûrement depuis très longtemps l'inégalité triangulaire en math : puisque (2-1)<90° comme sur ton schéma, tu as nécessairement :
I<I1+I2
La longueur du coté "vert" de ton triangle est nécessairement inférieure à la somme des longueurs des côtés "noir" et "rouge" !
L'égalité I = I1+I2 serait obtenue dans le cas particulier de deux intensités instantanées en phase : 1 = 2
Cela dit, comme la valeur de (2-1) est assez faible, l'écart relatif entre I et (I1+I2) n'est pas très important : 0,72% mais avec deux moteurs de puissances très différentes, l'écart relatif pourrait être important !
Je suis d'accord avec tes calculs.

Posté par
lachgar2re : Courant efficace utilisant Fresnel 09-01-17 à 18:17

Bonjour .
Peut on dire que I = I1 +I2

Posté par
lachgar2re : Courant efficace utilisant Fresnel 09-01-17 à 18:20

lachgar2 @ 09-01-2017 à 18:17

Bonjour .
Peut on dire que I = I1 +I2


D'accord j'ai compris .
Merci

Posté par
J-Pre : Courant efficace utilisant Fresnel 09-01-17 à 20:01

Dans un moteur, le courant est en retard sur la tension.

Donc pour M1, I1 est en retard de 45,57° sur la tension U
et pour M2, I2 est en retard de 31,78° sur la tension U

De cela, on conclut que I1 est en retard de (45,57 - 31,78) = 13,79° sur I2

Alors, pourquoi sur le dessin, dessines-tu I1 en avance sur I2 ?

Certes, tout est question de conventions ... mais autant choisir la plus largement repandue.

Me trompe-je ?


Posté par
lachgar2re : Courant efficace utilisant Fresnel 09-01-17 à 22:36

J-P @ 09-01-2017 à 20:01



Alors, pourquoi sur le dessin, dessines-tu I1 en avance sur I2 ?



parce que  cos\phi _{1}\prec cos\phi _{2}\Rightarrow \phi _{1}\succ \phi _{2}  sur  \left\{0,\frac{\pi }{2} \right\} et  le  sens  positif  est  le  trigonométrique

Posté par
lachgar2re : Courant efficace utilisant Fresnel 09-01-17 à 23:05

Je pense avoir compris ce que vous voulez dire (sur le dessin)
Mais, ça veut il dire que mon dessin est faux ?

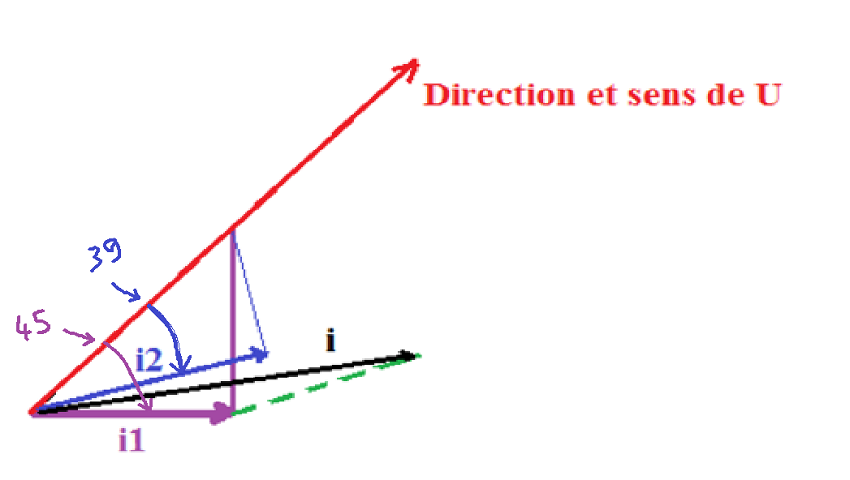
Courant efficace utilisant Fresnel

Posté par
J-Pre : Courant efficace utilisant Fresnel 10-01-17 à 13:05

Ton dessin donne tous les angles "à l'envers".

Ce qui donne les mêmes réponses en valeur efficace pour i et des mesures d'angles tous avec un mauvais signes... mais de bonnes amplitudes.

Enfin, il me semble que si on emploie un diagramme de Fresnel, on devrait respecter le sens des angles (suivant la convention la plus largement répandue)

Et comme dans un moteur, le courant est en retard sur la tension ... c'est mon dessin qui est dans le "bon sens"

Sauf distraction.  

Posté par
lachgar2re : Courant efficace utilisant Fresnel 10-01-17 à 13:30

D'accord .Merci beaucoup.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !