Inscription / Connexion Nouveau Sujet
corps solide, angle thêta
Bonjour,
je suis en première année de médecine et j'ai un exercice à faire et je ne sais pas très bien par où commencer.
Le problème est " Un yoyo a un rayon extérieur R et un rayon intérieur r et une masse M. A partir de quel angle le yoyo se met-il à rouler sans glisser ? le coefficient de frottement statique est
. "
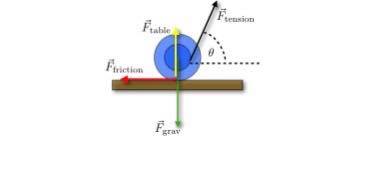
Il y a un schéma joint avec où les différentes forces la force gravitationnelle qui s'exerce vers le bas, la force de la table ou est posé le yoyo qui s'exerce inversement à la force gravitationnelle, la force de friction qui s'exerce perpendiculairement à la table vers la gauche. Le yoyo est constitué de deux rond un dans l'autre, et l'angle
est formé à partir du rayon du plus grand rond et de la force de tension F qui s'exerce vers le haut.
Merci d'avance à la personne qui me repondra 
Bonjour
Peux tu scanner et poster le schéma (format png ou jpeg) ? Difficile sinon de t'aider de façon efficace.
OK merci !
Tu ne définis pas l'accélération du centre du yoyo par rapport à la table. J'imagine que le centre du yoyo est d'accélération suffisamment faible pour que le produit (masse x accélération) soit négligeable devant les intensités des forces : il est alors possible de traiter le problème en considérant cette accélération comme nulle. Tu peux ainsi considérer que, pendant la phase de glissement, le yoyo est en mouvement de translation rectiligne uniforme par rapport à la table. La somme des quatre vecteurs forces appliquées au yoyo est alors le vecteur nul. En projetant cette relation vectorielle sur un axe vertical puis un axe horizontal, tu vas obtenir deux relations faisant intervenir les norme des quatre vecteurs forces et l'angle 
.
Pour obtenir la réponse demandée, il suffit ensuite d'appliquer la loi de Coulomb sur les frottements entre solides. Dans le cas d'un glissement la norme de la réaction tangentielle et la norme de la réaction normale vérifient l'inégalité :
Ffriction 
s.Ftable
Je te laisse réfléchir à tout cela et, j'espère, obtenir le résultat. Sinon, n'hésite pas à demander une aide supplémentaire.
Merci beaucoup de l'aide je vais essayer avec ces infos puis je reviendrais vers vous si j'ai quelques soucis
j'ai un peu de mal
Cela ne m'étonne pas ! Plutôt compliqué à ce niveau ! As-tu étudié le théorème du moment cinétique , la notion de moment d'inertie par rapport à un axe et la notion de moment de force par rapport à un axe ? Si oui, les choses sont assez simples, sinon...
Oui on l'a étudié
Tant mieux ! Dans ces conditions,il est possible d'étudier directement le mouvement de roulement sans glissement sans faire les approximations évoquées dans mon message précédent. Je suppose d'abord que la force de traction fait tourner le yoyo autour d'un axe (Oz) perpendiculaire au plan de figure dans le sens antihoraire que nous prendrons comme sens positif, la vitesse de rotation du yoyo autour de cet axe est notée
, l'accélération angulaire étant d/dt. Le fil se déroule sur le yoyo. S'il n'y a pas de glissement, cette rotation entraîne un mouvement du centre O du yoyo vers la gauche avec une accélération par rapport à la terre notée a, la vitesse de O étant notée V.
La condition de roulement sans glissement s'écrit : V = R.
soit par dérivation par rapport au temps : a = R.d/dt.
La relation fondamentale de la dynamique en projection sur un axe horizontal orienté vers la gauche conduit à :
(1) :
En notant J le moment d'inertie par rapport au yoyo, le théorème du moment cinétique conduit à :
(2) :
Division de tous les termes par R :
(3) :
Par addition membre à membre de (1) et (3) :
(4) :
Puisque Ftraction>0 et a
0, la relation précédente conduit à :
(5) :
Que se passe-t-il si la condition précédente n'est pas remplie, c'est à dire si l'angle
est suffisamment faible pour que l'on ait : Les formules précédentes conduisent à a<0 : le mouvement est encore un roulement sans glissement mais en sens inverse : le fil s'enroule sur le yoyo au lieu de se dérouler, le yoyo roule en sens horaire, son centre se déplace vers la droite. Je trouve donc la question posée par ton énoncé plutôt ambiguë... Tu peux vérifier cela expérimentalement très simplement si tu disposes chez toi d'un yoyo ou à défaut d'une simple bobine de fil à coudre.
Telle que la question est posée, je crois que tu peux t'arrêter là. Pour approfondir, on peut se demander à quelle condition on obtient un glissement. Pour cela, on peut projeter la relation fondamentale de la dynamique sur un axe vertical :
(6) :
L'absence de glissement impose (loi de Coulomb) :
(7) :
(attention : dans mon message précédent, j'ai commis une étourderie : j'ai écrit condition de glissement au lieu de condition d'absence de glissement)... Il est alors possible de montrer que le roulement sans glissement n'est possible que si la force de traction reste inférieure à une certaine valeur qui dépend de
S, , M, g, r, R et J...
Si la force de traction est supérieure à celle donnée par l'expression précédente, il y a glissement.
J'ai eu, pendant plusieurs années récentes, l'occasion d'aider en physique des étudiants en médecine : cet exercice me parait d'un niveau bien élevé... Certaines justifications de formules te paraissent peut-être un peu "rapides", je n'ai pas refait de schéma détaillé.... N'hésite pas à poser des questions supplémentaires si tu le juges nécessaire.
Pour info mais, comme déjà expliqué, sans doute pas indispensable, sauf erreur de calcul de ma part, la condition de roulement sans glissement suppose :
Si cette condition n'est pas vérifiée ( si tu tires trop fort sur le fil) un phénomène de glissement apparaît.
Tu es bien sûr que cet exo a été donné par ton professeur ?
Je n'ai peut-être pas été assez précis sur le cas particulier . Il correspond à une accélération et une accélération angulaire nulles. Deux cas sont possibles :
* soit le yoyo est initialement immobile : dans ce cas : il y reste pour peu bien sûr que l'intensité de la force de traction reste inférieure à la valeur indiquée au-dessus pour ne pas glisser.
* soit le yoyo est initialement animé d'un mouvement initial vers la droite ou vers la gauche : ce moment persiste avec une vitesse et une vitesse angulaire constantes.
Je viens tout juste de voir votre réponse ! Merci beaucoup de tout ce détail je vais me pencher correctement dessus mais j'ai déjà un peu plus compris avec les formules et les explications c'est plus clair dans ma tête. Oui oui c'est bien mon professeur qui nous à donné ça a faire mais j'irai vers lui avec l'ambiguïté que vous m'avez exposé.
Au cas où ton professeur ne serait pas convaincu, essaie de mettre dans ta poche un yoyo ou une bobine de fil. L'expérience est très rapide et très démonstrative.
Si tu tires faiblement sur le fil faiblement incliné par rapport à l'horizontale, la bobine roule sans glisser vers la droite (cf ta figure)
Si tu tires faiblement sur le fil fortement incliné par rapport à l'horizontale, la bobine roule sans glisser vers la gauche.
Si tu tire brutalement sur le fil, un phénomène de glissement apparaît.
Annuler
connectez vous