Inscription / Connexion Nouveau Sujet
Corde plombée, onde stationnaire
Bonsoir, pourriez vous juste m'expliquer un point d'un exercice que je n'ai pas compris?
Merci d'avance!
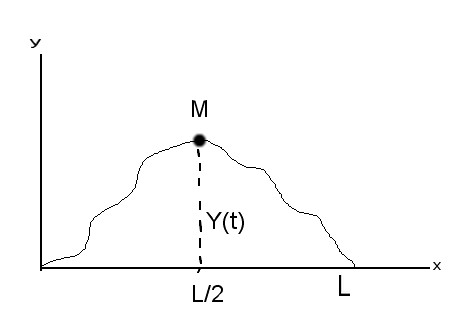
La corde ci dessous est plombée en son milieu M par une masse m. On néglige la pesanteur et la corde, fixée à ses deux extrémités, est tendue avec la tension T0 quand l'ensemble est au repos.
Etudier les petits mouvements transversaux de la masse m repérés par la position Y(t).
=> Dans le correction on propose tout d'abord d'écrire l'élongation comme une onde stationnaire:
pour x€[0,L/2] y(x,t)=y1(x,t)=A1sin(kx)cos(wt)
pour x€[L/2] y(x,t)=y2(x,t)=A2sin(k(L-x))cos(wt)
Ma question est toute simple, et la réponse l'est sûrement encore plus...: pourquoi k(L-x) dans la seconde expression et pas k(L/2-x)[d'accord ça ne collerait pas en x=L/2 mais ça ne m'explique pas le résultat]
Autre chose: ne peut-on pas au lieu d'exprimer l'onde comme une onde stationnaire l'exprimer comme la somme d'une onde plane progressive harmonique incidente et réfléchie pour x€[0,L/2] et comme une OPPH transmise pour x€[L/2]?
Bonjour,
Cela est du aux conditions aux limites quand tu résous en stationnaires l'équation de d'Alembert. En effet, tu as y(0,t) = 0 et y(L,t) = 0 (Et non L/2). Voilà pourquoi.
Si tu as d'autres questions, n'hésite pas.
Bonsoir,
Oui j'ai remarqué que ça ne collerait pas en x=L/2 mais est ce que ça justifie le fait que l'expression y(x,t)=y2(x,t)=A2sin(k(L-x))cos(wt) est valable également pour x strictement supérieur à L/2 ?
Bonsoir,
Ce que tu dis n'as pas de sens. Pour le moment, tu as juste à identifier les conditions aux limites pour y(x,t) pour la solution stationnaire de l'onde dans l'équation de d'Alembert. Et ça te donne de solutions distinctes car ton équation n'est valable que pour une corde homogène (la masse crée une inhomogénéïté dans la masse linéïque de la corde).
Oui je comprends que par le fait que la corde est plombée, on a 2 solutions distinctes pour l'élongation; mais je ne vois pas ce qui justifie l'expression de y(t) après le plombage. Ca ne me viendrait pas spontanément donc j'essaie de comprendre pourquoi !
Bonjour Dilettante,
Le pourquoi physique provient pas tant de la masse que tu as deux conditions aux limites qui sont à priori incompatibles. Après, là où la masse entre en jeu, c'est que c'est plus simple de résoudre l'équation de d'Alembert quand la masse linéique est constante.
Commence par me montrer comment tu résous l'équation de D'Alembert. Puis à l'aide de y(t,0) = 0, tu me donneras le calcul qui t'a conduit à la première équation. En voyant ton travail en entier, il me sera plus facile de cerner où sont tes problèmes.
Bonsoir Boltzmann_Solver,
Pour la première équation, on cherche une solution sous la forme d'onde stationnaire donc y(x,t)= A cos(wt + a)cos(kx + b)
On a en x=0 y(0,t)=0 donc cos(b)=0 b=0[Pi]
D'où y(x,t)=A cos (wt +a) sin (kx)
On exprime ensuite la condtion aux limites en x=L/2 Y(t)=Acos(wt+a)sin(kL/2)
On fait de même avec l'autre équation et on applique ensuite le PFD à la masse m pour résoudre entiérement. Je sais à peu près comment le faire c'est juste cette 2eme équation qui me perturbe! (et pourquoi a t-on a=0?)
Bonsoir dilletante,
Là, tu dépasses le cadre de ta question. A savoir le pourquoi des conditions aux limites. Si tu veux plus d'aide, il va falloir que tu précises tes soucis ! En grand seigneur, j'ai rédigé le début. A toi de me dire ou tu bloques ensuite.
1) Tu as un fil tendu aux deux extrémités. Donc, y(0,t) = 0 et y(L,t) = 0 et cela pour tout t.
Donc, la nature des conditions aux limites nous pousse à choisir une équation stationnaire de la forme : y(x,t) = A*cos(wt+a)*cos(kx+b). Cependant, la masselote rend la résolution que sur [0,L/2[ ou ]L/2,L].
Ces deux conditions aux limites nous donne à priori deux expressions à savoir.
y(0,t) = 0 <==> cos(kx+b) = 0 <==> b = pi/2 mod pi ==> y1(x,t) = A*cos(wt+a)*cos(kx+pi/2 mod pi) = A'*cos(wt+a)*sin(kx) avec A' dans R avec A=+/-A'
y(L,t) = 0 <==> cos(kL+b) = 0 <==> kL+b = pi/2 mod pi <==> b = -kL + pi/2 mod pi ==> y2(x,t) = B*cos(wt+a)*cos(kx+pi/2 mod pi - kL) = B'*cos(wt+a)*sin(k(x-L)).
C'est bien ce que te donne ta correction, non ?
Ensuite, il faut relier ces équations.
On sait par continuité que :
lim_{x---> L/2-} y1(t,x) = lim_{x---> L/2+} y2(t,x) <==> A'*cos(wt+a)*sin(kL/2) = B'*cos(wt+a)*sin(kL/2) <==> (A'-B')*cos(wt+a)*sin(kL/2) = 0.
Ca, j'ose croire que tu as compris.


