Inscription / Connexion Nouveau Sujet
Coordonnées, produit vectoriel
Bonsoir,
L'énoncé de l'exercice est le suivant :
Un pendule formé d'un point matériel pesant de masse m et d'un fil sans masse de longueur L est astreint à osciller sans frottement dans le plan d'une porte qui tourne d'un axe vertical à vitesse angulaire  constante. Le pendule est attaché au point O à l'axe de rotation de la porte et le fil fait un angle
constante. Le pendule est attaché au point O à l'axe de rotation de la porte et le fil fait un angle  avec cet axe. Par rapport au référentiel absolu R du laboratoire, le référentiel relatif R', dans lequel la porte est au repos, tourne à vitesse angulaire
avec cet axe. Par rapport au référentiel absolu R du laboratoire, le référentiel relatif R', dans lequel la porte est au repos, tourne à vitesse angulaire  constante.
constante.
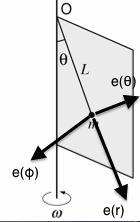
On demande de faire le bilan des forces, ça ok, puis de les projeter selon le repère tournant O,er,e ,e
,e (voir figure).
(voir figure).
Je bloque concernant la projection des forces centrifuge et de Coriolis.
L'expression de la force centrifuge est F = -m
 (
(
 OP )
OP )
Et Coriolis : -2m


Le souci est que je ne trouve pas les coordonnées du vecteur OP ni du vecteur  pour ainsi faire le produit vectoriel et conduire aux équations de mouvements.
pour ainsi faire le produit vectoriel et conduire aux équations de mouvements.
Cela peut paraître idiot mais je me casse les dents dessus.
La réponse pour la projection de la force centrifuge est (en gras indique vecteur) : mL 2sin(
2sin( ) . (sin(
) . (sin( er + cos (
er + cos ( ) e
) e )
)
Merci d'avance et bonne soirée.
J'ai finalement compris, les coordonnées de  sont (-
sont (- cos
cos ,
,  sin
sin ,0) et pour la vitesse
,0) et pour la vitesse  : (0, L.
: (0, L. "point",0).
"point",0).
Et cela fonctionne



