Inscription / Connexion Nouveau Sujet
Coordonnées cartésiennes à cylindriques
Bonjour, je cherche à écrire les coordonnées d'un champ de vecteurs en coordonnées cylindriques.
Soit .
J'ai essayé d'exprimer ,
et
en cylindrique, sans grand succès.
Auriez-vous quelques indications pour moi ?
Merci d'avance.
Bonsoir,
Utilise les conversions: x=r*cos(teta) et y=r*sin(teta) et z reste z
Ensuite on fait apparaitre le vecteur radial ur = cos(teta)*ex+sin(teta)*ey
Mais il y a un probleme pour faire apparaitre le vecteur ur.Il n'y a pas une erreur ?
Comment je me sers de ces conversions ? Là on a les coordonnées en cartésiennes donc on a déjà x y et z. Il faut isoler r et ?
Quel est le problème pour faire apparaître le vecteur radial ?
le but est bien de changer x ,y , z aussi mais ici il est absent.
On a r*sin(teta)*ex+r*cos(teta)*ey+r*(cos(teta))^2*ez.
La base en cylindrique est ( ur, uteta ,uz).
Sachant que ur = cos(teta)*ex+sin(teta)*ey et uteta = -sin(teta)*ex+cos(teta)*ey
Je ne vois pas comment on peut continuer.
Bonjour à tous les deux
On peux commencer par réfléchir à la pertinence de ce changement de système de coordonnées. On sait que les coordonnées cylindriques sont particulièrement adaptées aux problèmes présentant une symétrie par rapport à l'axe (Oz). Soit M(x,y,z) et M'(-x,-y,z) le point symétrique par rapport à (Oz).
La composante suivant z de est la même en M et en M' alors que les composantes suivant x et y changent de signe alors que passer de M en M' remplace
par son opposé et remplace
par son opposé. Le changement de système de coordonnées peut sembler pertinent...
Ce qu'à écrit raptor666 est correct mais je ne vois pas de problème particulier concernant .
Les calculs se simplifient bien en faisant intervenir l'angle double...
z aussi mais ici il est absent
Cela signifie simplement que le champ de vecteur
Merci vanoise pour ces éclaircissements !
Je n'arrive pas à retrouver les relations que tu as données dans ta réponse, comment fait - on ?
En appliquant ta formule, je trouve .
Etes-vous d'accord ?
Ah ben oui
J'avais oublié de convertir ex,ey et ez dans la base cylindrique.
Voilà pourquoi cela m'a embrouillé ! autant pour moi.
D'accord avec ton résultat. Tu peux éventuellement remplacer le cos2 par une expression faisant intervenir le cosinus de l'angle double pour un résultat plus homogène mais cela n'est pas obligatoire.
Je n'arrive pas à retrouver les relations que tu as données dans ta réponse, comment fait - on ?
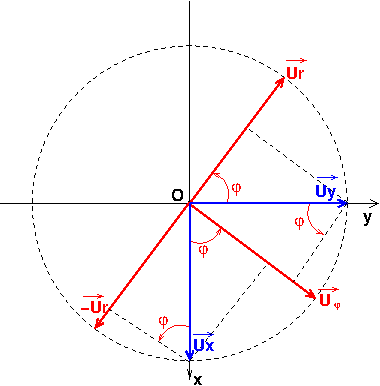
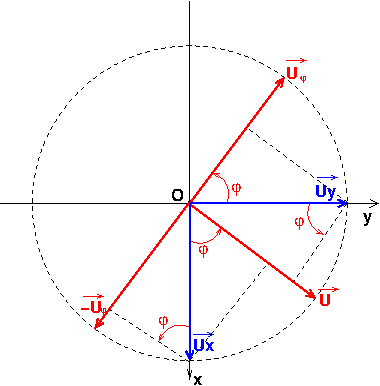
Voici, sous forme de schémas, un rappel sur les coordonnées cylindriques puis une représentation des vecteurs unitaires qui te posent problème. Il s'agit de simples projection comme tu as appris à en faire dans l'enseignement secondaire.
PS : J'ai l'habitude de noter "u" un vecteur unitaire plutôt que "e" comme cela se fait aussi. Cela ne devrait pas te perturber je pense.
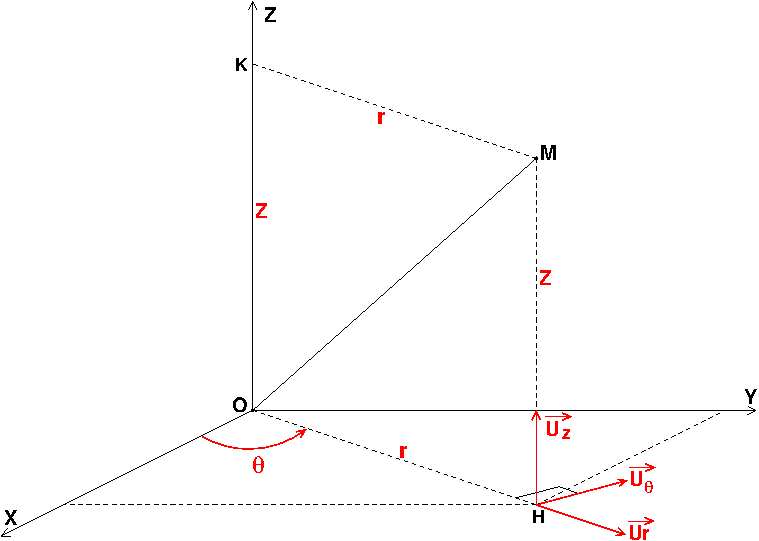
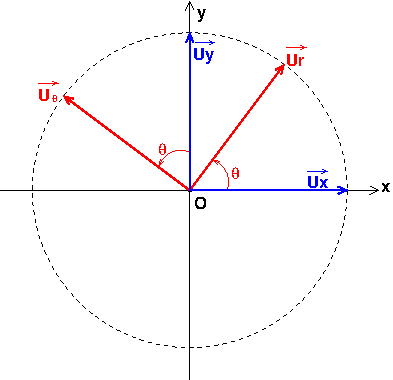
On peut aussi retrouver l'expression des vecteurs unitaires du repère cartésien selon les vecteurs unitaires du repère sphérique de la même manière ?
Bien sûr ! Toujours la même méthode de projection ! Il faut t'entraîner à faire cela de façon rapide et fiable car ce genre de projection intervient très souvent !
Auriez-vous l'expression ces vecteurs ? Je n'arrive pas à les trouver ailleurs pour vérifier ce que j'ai trouvé.
Si je comprends bien, tu t'intéresses maintenant aux coordonnées sphériques.
Méthode possible :
Commencer par exprimer les vecteurs et
en fonction de
et
: vecteur unitaire ayant la direction et le sens de
sur le schéma.
Ce vecteur s'exprime ensuite assez facilement en fonction de
et
ensuite.
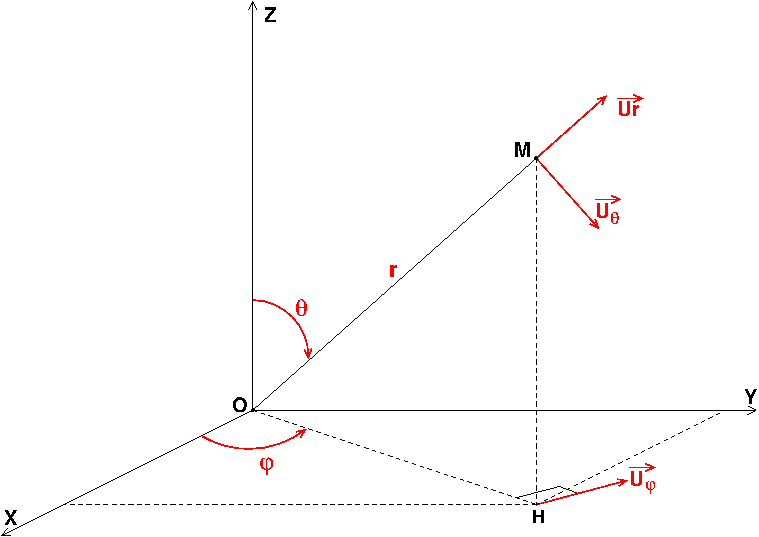
Je pensais maîtriser mais j'en suis plus trop sûr maintenant...
On a la même expression pour mais je ne suis pas certain d'avoir la bonne méthode pour le trouver. Et je n'arrive pas à retrouver votre expression pour
.
Ce que je fais c'est que je retrouve sur mon schéma et je fais la trigo dans le triangle rectangle rouge sur l'image :
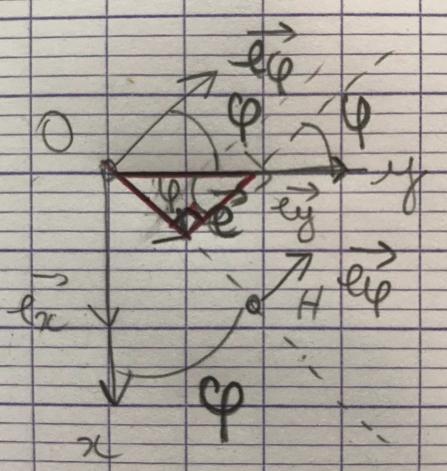
Merci pour les représentations des différents emplacements de l'angle, c'est ça qui me posait problème.
Je trouve donc :