Inscription / Connexion Nouveau Sujet
Convolutions
Bonjour,
Actuellement en 3eme année de licence, j'aurais besoin d'un peu d'aide car je n'est pas très bien compris le cours sur les convolutions et le professeur m'a donné quelques exercices à faire cependant ayant déjà des difficultés à saisir le cours, les exercices me paraissent totalement flou. Alors en espérant tomber sur une personne qui aurait le temps de m'expliquer un peu plus en détails ces exo et m'expliquez un peu plus clairement les notions du cours q ce serait vraiment gentil de sa part.
Merci de votre aide 
Partie A :
1) Filtre dérivateur
On modélise la réponse impulsionnelle de ce filtre par :
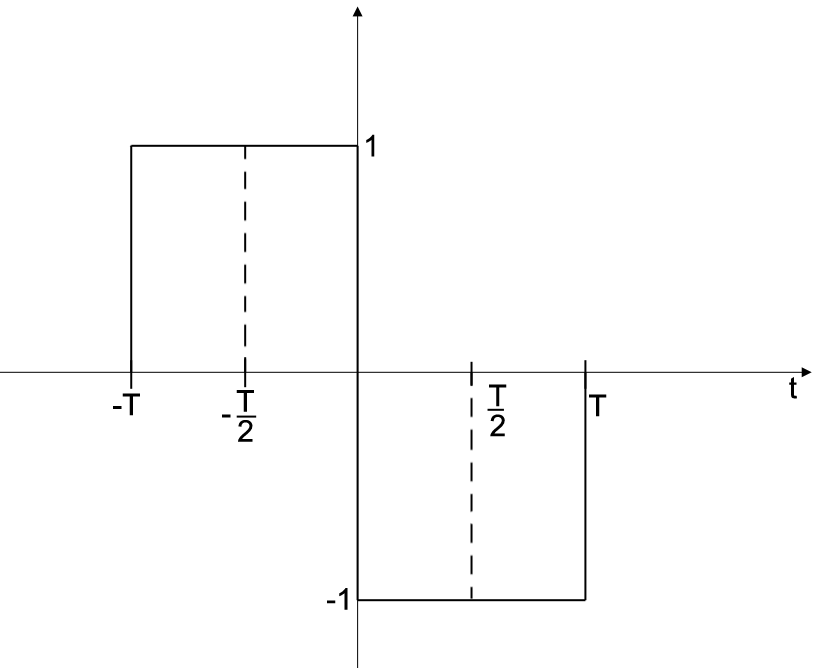
h(t) = rect(t/T + 1/2) - rect(t/T - 1/2), T > 0
a) Représenter graphiquement h(t), en indiquant les abscisses importantes.
b) Ce filtre est-il causal ? Pourquoi ?
c) Soit un signal défini par : f(t)=2 rect((t-4T)/8T)
.
Donner graphiquement le résultat de la convolution de ce signal par la réponse impulsionnelle du filtre.
En quoi ce filtre est-il dérivateur ?
d) Calculer la fonction de transfert de ce filtre.
2) Calculer l'intégrale de (-l'infini à +l'infini) de [ (sin(2pi.(t/T)) / (2pi.(t/T)) ]^2 dt , T >0
3) Calculer la transformée de Fourier de la fonction f(x)= x rect (x)
Partie B :
1) Calculer intégrale de (-l'infini à +l'infini) de (sin(x)/x)^2 dx
2) Calculer intégrale de (-l'infini à +l'infini) de exp(-x^2) dx
3) Filtre dérivateur
On modélise la réponse impulsionnelle de ce filtre par :
h(t) = rect(t/T + 1/2) - rect(t/T - 1/2), T > 0
a) Représenter graphiquement h(t), en indiquant les abscisses importantes.
b) Ce filtre est-il causal ? Pourquoi ?
c) Soit un signal défini par : f(t)=y0 rect(t/6T)
.
Donner graphiquement le résultat de la convolution de ce signal par la réponse impulsionnelle du filtre.
En quoi ce filtre est-il dérivateur ?
d) Calculer la fonction de transfert de ce filtre.
Partie C :
1) On désire réaliser un filtre passe-bas parfait de fonction de transfert h^(v)=rect(v/2v0), avec v0>0.
- Calculer sa réponse impulsionelle.
- Ce filtre est-il réalisable en temps réel ? Justifier votre réponse.
2) a) Représenter graphiquement en graduant l'axe des abscisses et l'axe des ordonnées la fonction :
f(x) = rect(x/2) + rect((x-5)/2)
b) Calculer et représenter graphiquement, en graduant l'axe des abscisses et l'axe des ordonnées, la fonction g(x) = f(x) * f(-x ). Vérifiez votre résultat : que pouvez vous dire sur la parité de g(x) ? Pourquoi ?
Merci de votre liens pour ce qui est du cours, ca me parait un peu plus clair ^^
Cependant, si quelqu'un pouvais m'aider a faire ces exo :&
h(t) = rect(t/T + 1/2) - rect(t/T - 1/2), T > 0
Pour y voir plus clair , il faut écrire :
Ou encore :
Il s'agit donc de 2 fonctions portes de largeur T décalée pour la 1ère de
OK ?
Et la 1b ?
Merci pour cette reponse pour la premiere question Aragorn 
Pour ceux qui est de la 1.b) je sais que par définition :
Une fonction f est causale si pour tout réel x strictement négatif ,
f(x) = 0
Donc, dans notre cas, pour cette fonction la fonction n'est pas causale.
C'est exact...
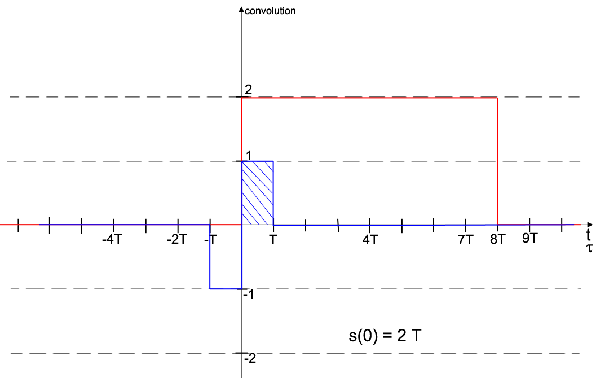
Pour la 1c, f(t)=2 rect((t-4T)/8T) est donc une fonction porte centré sur 4T et de largeur 8T. La fonction porte va donc de 0 à 8T.
Pour obtenir graphiquement le résultat de la convolution h(t) * f(t), as-tu une idée ?
" une fonction porte centré sur 4T et de largeur 8T." ==> une fonction porte centrée sur 4T et de largeur 8T et d'amplitude 2.
Ah nan pardon, on me demande graphiquement, donc il faut aussi que je représente la fonction h(t) graphiquement.
PS : Encore merci de m'aider 
Oh et je viens de m'apercevoir que vous vous êtes trompez avec l'énonce sur la fonction de h(t) qui est
h(t)= rect( (t/T) + 1/2 ) - rect( (t/T) - 1/2 ) 
C'est exactement ce que j'ai écrit...
h(t)= rect( (t/T) + 1/2 ) - rect( (t/T) - 1/2 )
On réduit au même dénominateur :
Que l'on peut écrire :
Ou encore :
Donc la 1ère est une fonction porte décalée de et la 2ème, une fonction porte décalée de
.
Donc il n'y a pas d'erreur.
Il est aussi possible de faire un changement de variable en posant mais je ne cois que ce soit avantageux.
La 2ème fonction porte est inversée à cause du signe - .
Donc on obtient le graphique que j'ai donné plus haut.
Il faut appliquer la définition de la convolution :
Si on prend la 1ère définition, signifie que l'on calcule le résultat à t mais le - devant
signifie que la fonction est inversée sur l'axe des temps.
Oups d'accord je n'avais pas fais attention au dénominateur commun. Ok maintenant c'est clair.
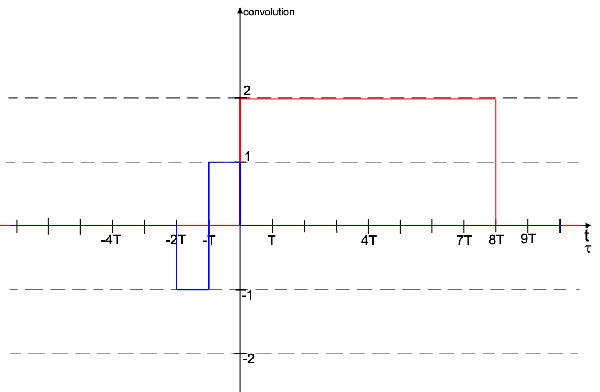
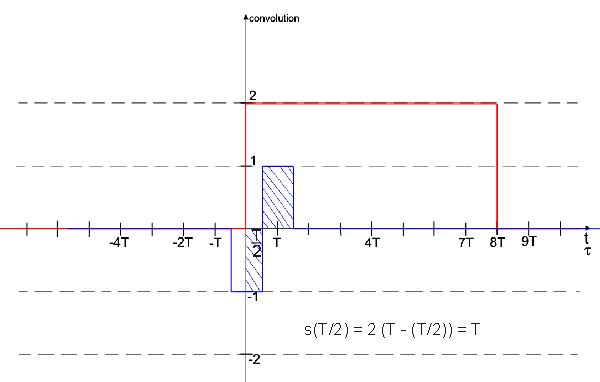
Alors ensuite pour t=T/2, s(T/2)=3T
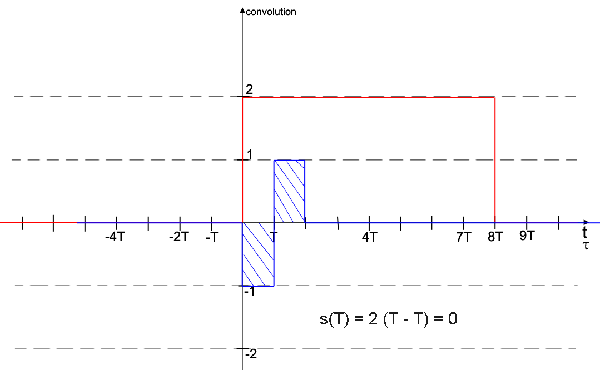
Lorsque t est pris entre T et 7T s(t)=0
Et ensuite vu que le rectangle négatif se retrouve uniquement avec h(t) alors on retrouve l'inverse des valeurs que l'on retrouve au début lorsque l'on translate le rectangle positif.
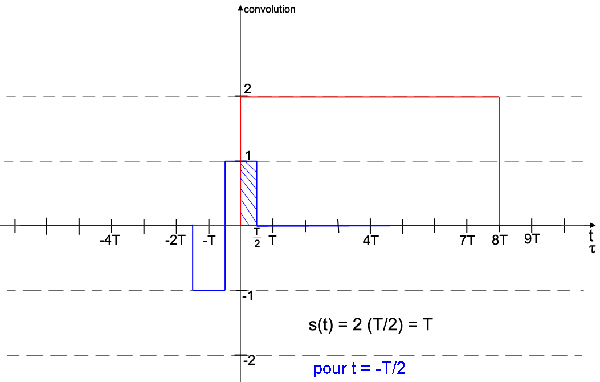
Alors ensuite pour t=T/2, s(T/2)=3T
Non, comme je l'ai écrit précédemment, s(T/2) = T parce que il y a une aire positive et une aire négative. Il faut revenir à la définition de base des intégrales.
Effectivement, pour T
 t
t  7T, s(t) = 0 .
7T, s(t) = 0 .
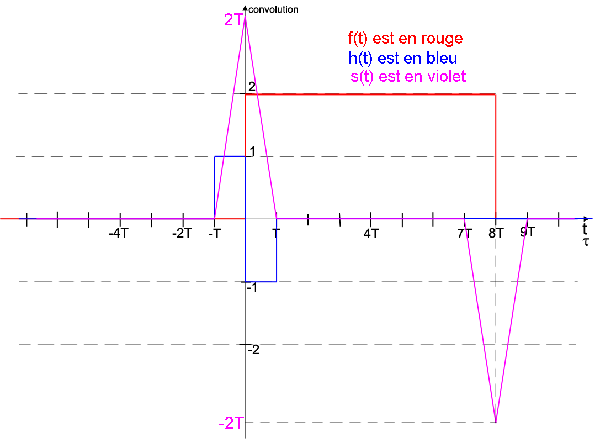
Et :
s(7T) = 0
s(8T) = -2T
s(9T) = 0
Es-tu d'accord avec ça ?
Oui je viens de m'en rendre compte maintenant en faisant la représentation graphique j'obtiens deux triangles inverses.
Pour le dernier triangle, en 7T j'obtiens bien 0 puis pour 8T bien 2T et pour 9T bien 0.
En tout cas, merci beaucoup pour votre patience, vos explications et vos graphes clairs et soignés 

Pour ce qui est de dire en quoi ce filtre est dérivateur, je ne vois pas..
La dérivée de f(t)est composée de 2 impulsions de Dirac, l'une positive en t = 0 et l'autre négative en t = 8T. Mathématiquement, la dérivée est infinie en t = 0 et t = 8T mais, au sens des distributions, il s'agit de 2 impulsions de Dirac.
Les 2 pointes que l'on a obtenues, ressemblent à 2 impulsions de Dirac. Le filtre dérivateur n'est pas parfait à cause de la largeur des fonctions portes donc les impulsions de Dirac sont plus larges. Plus les fonctions portes seront étroites et plus les impulsions obtenues seront étroites.
Il s'agit donc bien d'un filtre dérivateur (certes imparfait).
Il faut que je calcul la TF du produit de convolution.
En particulier je sais que : s(x)= e(x)*h(x)
s(x)= e^(x)*h^(x)
h^(x) étant la fonction de transfert du système, TF de la réponse impulsionnelle, c'est ça ?
Ce n'est pas la TF d'un produit de convolution.
Il faut calculer la fonction de transfert du filtre. On sait que c'est la TF de la réponse impulsionnelle.
Donc il faut calculer la réponse impulsionnelle de h(t).
.
h(t) se sépare en deux.
et
Il faut donc utiliser la TF de et ensuite la TF de
"Donc il faut calculer la réponse impulsionnelle de h(t)." ==> Donc il faut calculer la TF de la réponse impulsionnelle de h(t).
Pas facile à lire mais je crois que c'est ça...
Je le réécris de façon plus lisible :
Et si on fait la somme (ou plutôt la différence) ?

 fa . h^(f)
fa . h^(f)

