Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Posté par
Aragornre : Convolutions 10-11-14 à 19:33

On se demande un peu ce que ça vient faire là mais

Citation :
2) Calculer l'intégrale de (-l'infini à +l'infini) de [ (sin(2pi.(t/T)) / (2pi.(t/T)) ]^2 dt   , T >0

Posté par
gigi7o 10-11-14 à 20:33

Ben j'ai demander au prof de me donner des exercices,
typique examen!

Posté par
Aragornre : Convolutions 10-11-14 à 20:38

OK, pas de soucis...
Là, c'est un peu compliqué. As-tu une idée ?

Posté par
Aragornre : Convolutions 10-11-14 à 22:47

On calcule la transformée de Fourier inverse d'une fonction porte de largeur 2f0 divisée par 2f0:
\Large \int_{-\infty}^{+\infty}\frac{1}{2f_0}\,rect\left(\frac{f}{2f_0}\right)\,e^{j2\pi ft}
On peut montrer que c'est égal à :
\Large \frac{sin\left(2\pi f_0t\right)}{2f_0\pi t}
En posant   \frac{1}{T}\,=\,f_0  , on trouve :
\Large \frac{sin\left(2\pi\frac{t}{T}\right)}{2\pi \frac{t}{T}}
Ce qui nous intéresse, c'est :
\Large \left(\frac{sin\left(2\pi\frac{t}{T}\right)}{2\pi \frac{t}{T}}\right)^2\,=\,\left|\left(\frac{sin\left(2\pi\frac{t}{T}\right)}{2\pi \frac{t}{T}}\right)^2\right|\,=\,\left|\frac{sin\left(2\pi\frac{t}{T}\right)}{2\pi \frac{t}{T}}\right|^2
On peut alors appliquer l'égalité de Bessel-Parseval :
\Large \int_{-\infty}^{+\infty}\left|x(t)\right|^2dt\,=\,\int_{-\infty}^{+\infty}\left|X(f)\right|^2df
avec :
\Large x(t)\,=\,\frac{sin\left(2\pi\frac{t}{T}\right)}{2\pi \frac{t}{T}}
et :
\Large X(f)\,=\,\frac{1}{2f_0}\,rect\left(\frac{f}{2f_0}\right)
On peut alors calculer :
\Large \int_{-\infty}^{+\infty}\left|X(f)\right|^2df\,=\,\int_{-\infty}^{+\infty}\frac{1}{4f_0^2}\left|rect\left(\frac{f}{2f_0}\right)\right|^2df\,=\,\int_{-f_0}^{+f_0}\frac{1}{4f_0^2}df\,=\,\frac{1}{4f_0^2}\,\int_{-f_0}^{+f_0}df\,=\,\frac{1}{4f_0^2}\,2f_0\,=\,\frac{1}{2f_0}\,=\,\frac{T}{2}
Donc :
\Large \int_{-\infty}^{+\infty}\left(\frac{sin\left(2\pi\frac{t}{T}\right)}{2\pi \frac{t}{T}}\right)^2dt\,=\,\frac{T}{2}

Posté par
Aragornre : Convolutions 10-11-14 à 22:48

Citation :
3) Calculer la transformée de Fourier de la fonction f(x)= x rect (x)

Une idée ?

Posté par
gigi7ore : Convolutions 10-11-14 à 23:04

Ok merci pour votre réponse précédente.
Il fallait utiliser le théorème Perseval.  

Posté par
gigi7ore : Convolutions 10-11-14 à 23:10

Pour calculer la TF de x.rect(x) ai-je le droit de calculer d'abord la TF de x puis multiplier par la TF de rect(x)

Car je sais que la TF(rect(x))=sin[(v)/(v)]

Posté par
gigi7ore : Convolutions 10-11-14 à 23:14

TF(x.rect(x))= /[TF(rect(x))].1/2i
             = /[sin(].1/-2i

Posté par
Aragornre : Convolutions 11-11-14 à 01:14

Citation :
Pour calculer la TF de x.rect(x) ai-je le droit de calculer d'abord la TF de x puis multiplier par la TF de rect(x)

As-tu une formule qui dit : TF[x.rect(x)] = TF[x].TF[rect(x)] ?
La réponse est non...
Il faut calculer :
\Large \int_{-\infty}^{+\infty}\,x\,\,rect(x)\,e^{-2i\pi \nu x}\,dx

Posté par
Aragornre : Convolutions 11-11-14 à 01:17

avec :
\Large rect(x)\,=\,1\,\,\textrm{pour}\,\,-\,\frac{1}{2}\,\le\,x\,\le\,\frac{1}{2}\,\,\textrm{et}\,\,0\,\,\textrm{ailleurs}

Posté par
gigi7ore : Convolutions 11-11-14 à 08:44

de -1/2 a 1/2 de x.exp(-2ifx) dx

La j'applique une IPP :

On pose u'= exp(-i2fx) et u= exp(-i2fx) /(-i2fx)
v=x et v'=1
On applique la formule de l'IPP :

de -1/2 a 1/2 de exp(-2ifx).x= exp(-i2fx) /(-i2fx) .x de exp(-2ifx)

Ce qui donne :

[-1/(2ifx)](x-1)
D'ou
[-1/2ifx]((-1/2)exp(-if)-(3/2)exp(ifx)

Posté par
gigi7ore : Convolutions 11-11-14 à 09:27

Pour ce qui est de la question suivante :

∫∞−∞sin^2(x)/(x)^2 dx=π

On sait que sin^2(x)= [(1-exp(2ix)+(1-exp(2ix)]/4

D'ou :

∫∞−∞ sin2(x)/x2 dx
=∫∞−∞ (1−cos(2x))/2x^2 dx
=∫∞−∞ (1−e2ix)+(1−e−2ix)/4x^2 dx
=∫(1−e2ix)4x^2 dx + ∫(1−e−2ix)4x^2 dx
=2πi−(2i/4)+0
=π

C'est juste?

Posté par
gigi7ore : Convolutions 11-11-14 à 09:36

Pour ce qui est de exp(-x^2)

J'ai trouvé ceci qui pourra m'aider :

http://fr.m.wikipedia.org/wiki/Intégrale_de_Gauss

Posté par
Aragornre : Convolutions 11-11-14 à 11:10

Le début est bon
\Large \int_{-\frac{1}{2}}^{\frac{1}{2}}\,x\,e^{-2i\pi\nu x}\,dx   par définition de rect(x)
On peut appliquer une IPP effectivement :
\Large \int_{-\frac{1}{2}}^{\frac{1}{2}}\,x\,e^{-2i\pi\nu x}\,dx
\Large u\,=\,x\,\Rightarrow\,du\,=\,dx
\Large dv\,=\,e^{-2i\pi\nu x}\,dx\,\Rightarrow\,v\,=\,\frac{e^{-2i\pi\nu x}}{-2i\pi\nu}
donc  \int u\,dv\,=\,uv\,-\,\int v\,du   (tu peux remplacer les du et dv par u' et v' si tu préfères...)
\Large \int_{-\frac{1}{2}}^{\frac{1}{2}}\,x\,e^{-2i\pi\nu x}\,dx\,=\,\left[x\,\frac{e^{-2i\pi\nu x}}{-2i\pi\nu}\right]_{-\frac{1}{2}}^{\frac{1}{2}}\,-\,\int_{-\frac{1}{2}}^{\frac{1}{2}}\,\frac{e^{-2i\pi\nu x}}{-2i\pi\nu}\,dx
Essaye de faire le calcul et tu dois trouver :
\Large -\,\frac{1}{2i\pi}\,\frac{\pi \nu cos(\pi \nu)\,-\,sin(\pi \nu)}{\pi \nu^2}

Pendant ce temps, je vais essayer de décortiquer ton calcul...

Posté par
Aragornre : Convolutions 11-11-14 à 11:42

Apparemment, c'est dans l'application de l'IPP qu'il y a un problème...

Posté par
Aragornre : Convolutions 11-11-14 à 11:57

Citation :
=∫(1−e2ix)4x^2 dx + ∫(1−e−2ix)4x^2 dx
=2πi−(2i/4)+0

Là, j'ai un peu de mal à suivre...

Posté par
Aragornre : Convolutions 11-11-14 à 13:05

Citation :
1) Calculer intégrale de (-l'infini à +l'infini) de (sin(x)/x)^2 dx

Je pense qu'il vaudrait mieux utiliser une méthode similaire à la précédente pour  \large \frac{sin\left(2\pi\,\frac{t}{T}\right)}{2\pi\,\frac{t}{T}}^2
Si on calcule la transformée de Fourier de   \Large F(\nu)\,=\,\pi\,rect\left(\frac{\nu}{\frac{1}{\pi}}\right)   :
\Large F(\nu)\,=\,\int_{-\infty}^{+\infty}\,\pi\,rect\left(\frac{\nu}{\frac{1}{\pi}}\right)\,e^{2i\pi \nu x}\,d\nu\,=\,\int_{-\frac{1}{2}}^{+\frac{1}{2}}\,\pi\,e^{2i\pi \nu x}\,d\nu\,=\,\pi\,\left[\frac{e^{2i\pi \nu x}}{2i\pi x}\right]_{-\frac{1}{2}}^{\frac{1}{2}}\,=\,\pi\,\frac{e^{ix}\,-\,e^{-ix}}{2i\pi x}\,=\,\pi\,\frac{sin\,x}{\pi x}\,=\,\frac{sin\,x}{x}
Et :
\Large f(x)\,=\,\left(\frac{sin\,x}{x}\right)^2\,=\,\left|\left(\frac{sin\,x}{x}\right)^2 \right|\,=\,\left|\frac{sin\,x}{x} \right|^2
Egalité de Bessel-Parseval :
\Large \int_{-\infty}^{+\infty}\,\left|f(x)\right|^2\,dx\,=\,\int_{-\infty}^{+\infty}\,\left|F(\nu)\right|^2\,d\nu
Donc :
\Large \int_{-\infty}^{+\infty}\,\left(\frac{sin\,x}{x}\right)^2\,dx\,=\,\int_{-\infty}^{+\infty}\,\left|\frac{sin\,x}{x}\right|^2\,dx\,=\,\int_{-\infty}^{+\infty}\,\left|\pi\,rect\left(\frac{\nu}{\frac{1}{\pi}}\right) \right|^2\,d\nu\,=\,\int_{-\frac{1}{2}}^{+\frac{1}{2}}\,\pi ^2\,d\nu\,=\,\pi ^2\,\frac{1}{\pi}\,=\,\pi

Posté par
gigi7ore : Convolutions 11-11-14 à 13:47

Oui j'ai ete trop vite et j'ai oublier des termes..
Sinon en developpant ton calcul j'arrive a retrouver ce que vous m'avez mis.
Ah ok on fais le meme resonement que la question precedente!

Posté par
Aragornre : Convolutions 11-11-14 à 14:19

Citation :
2) Calculer intégrale de (-l'infini à +l'infini) de exp(-x^2)  dx

Je pense qu'il faut partir d'une transformée de Fourier connue :
\Large f(x)\,=\,e^{-\pi x^2}\,\Rightarrow\,F(\nu)\,=\,e^{-\pi \nu ^2}
(la transformée de Fourier d'une gaussienne est une gaussienne)
Moyennant un changement de variable, on peut trouver \int_{-\infty}^{+\infty}e^{-x^2}\,dx .
Je te mets la solution tout à l'heure à moins que tu ne l'aies trouvée...
      

Posté par
Aragornre : Convolutions 11-11-14 à 14:23

Mais on peut faire autrement...

Posté par
gigi7ore : Convolutions 11-11-14 à 17:53

Oula je ne vois pas comment procédé

Posté par
Aragornre : Convolutions 11-11-14 à 21:39

\Large F(\nu)\,=\,\int_{-\infty}^{+\infty}e^{-x^2}\,e^{-2i\pi \nu x}\,dx\,=\,\int_{-\infty}^{+\infty}e^{-u^2}\,e^{-2i\pi \nu \frac{u}{\sqrt{\pi}}}\,dx
\Large u^2\,=\,\pi x^2\,\Rightarrow\,x\,=\,\frac{u}{\sqrt{\pi}}
\Large x^2\,=\,\frac{u^2}{\pi}\,\Rightarrow\,2x\,dx\,=\,\frac{2u}{\pi}\,du\,\Rightarrow\,dx\,=\,\frac{u}{x}\,du\,\Rightarrow\,dx\,=\,\frac{u}{u}\sqrt{\pi}\,du\,=\,\sqrt{\pi}\,du
Donc :
\Large \int_{-\infty}^{+\infty}e^{-x^2}\,e^{-2i\pi \nu x}\,dx\,=\,\int_{-\infty}^{+\infty}e^{-u^2}\,e^{-2i\pi \frac{\nu}{\sqrt{\pi}} u}\,\sqrt{\pi} du\,=\,\sqrt{\pi}\int_{-\infty}^{+\infty}e^{-u^2}\,e^{-2i\pi \frac{\nu}{\sqrt{\pi}} u}\, du\,=\,\sqrt{\pi}\,e^{-\pi\frac{\nu^2}{\pi}}\,=\,\sqrt{\pi}\,e^{-\nu^2}
On a :
\Large \int_{-\infty}^{+\infty}e^{-x^2}\,dx\,=\,F(0)\,=\,\sqrt{\pi}

C'est au moins un moyen de le faire...

Posté par
Aragornre : Convolutions 11-11-14 à 21:55

Petite erreur, le changement de variable est incomplet...
\Large F(\nu)\,=\,\int_{-\infty}^{+\infty}e^{-x^2}\,e^{-2i\pi \nu x}\,dx\,=\,\int_{-\infty}^{+\infty}e^{-u^2}\,e^{-2i\pi \nu \frac{u}{\sqrt{\pi}}}\,\sqrt{\pi}\,du

Posté par
gigi7ore : Convolutions 12-11-14 à 06:38

J'avoue que la, je n'aurais jamais penser par faire par cette methode et en plus c'est source d'erreur si on se trompe dans le changement de variable :/

Posté par
gigi7ore : Convolutions 12-11-14 à 10:31

Pour ce qui est de la question 3) a) on mets au meme denominateur pour retrouver la meme fonction que dans la partie A.
3) b) pareil que la reponse en partie A.

3) c) on represente un rectangle damplitude y0 et de largeur 6T centrer en 0

Posté par
Aragornre : Convolutions 12-11-14 à 11:01

Citation :
3)  Filtre dérivateur

On modélise la réponse impulsionnelle de ce filtre par :
h(t) = rect(t/T + 1/2) - rect(t/T - 1/2), T > 0


a) Représenter graphiquement h(t), en indiquant les abscisses importantes.

b) Ce filtre est-il causal ? Pourquoi ?

c)  Soit un signal défini  par : f(t)=y0 rect(t/6T)
                   .
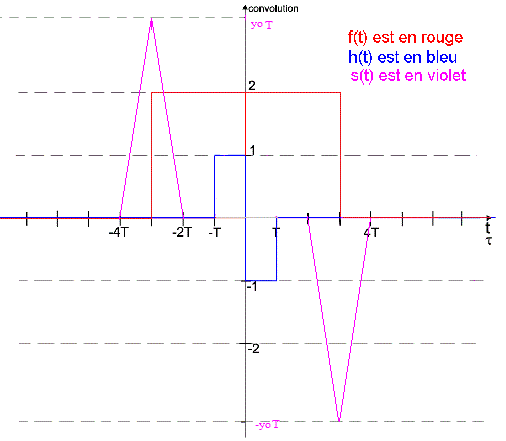
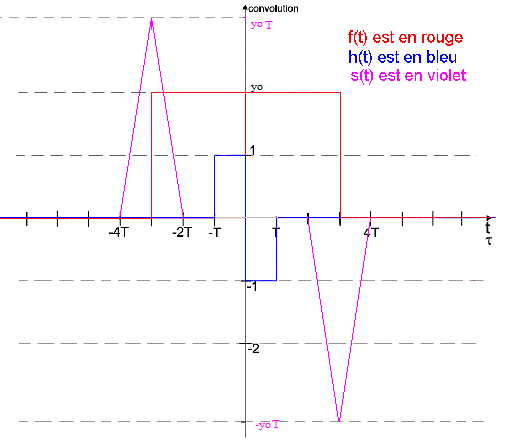
Donner graphiquement le résultat de la convolution de ce signal par la réponse impulsionnelle du filtre.

En quoi ce filtre est-il dérivateur ?

d) Calculer la fonction de transfert de ce filtre.

Oui, 3a et 3b même chose que la partie A.
Pour 3c, oui, c'est un rectangle d'amplitude y0 de largeur 6T et centré sur 0 c'est-à-dire qu'il va de -3T à + 3T.
Pour le résultat graphique de la convolution, la technique à utiliser est la même que précédemment.
filtre dérivateur ==> même chose que partie A.
Pour la fonction de transfert, c'est la transformée de Fourier de la réponse impulsionnelle.

Posté par
gigi7ore : Convolutions 12-11-14 à 11:09

D'accord je mettrais en fin de journee ce que j'ai trouvé et vous me direz si ce que j'ai fais et juste ou pas.

Posté par
gigi7ore : Convolutions 12-11-14 à 17:19

3a

Convolutions

Posté par
gigi7ore : Convolutions 12-11-14 à 17:21

Rectification de l'amplitude de f(t)

Convolutions

Posté par
gigi7ore : Convolutions 12-11-14 à 18:06

Pour ce qui est du calcul de la réponse impulsionnelle, je dis que : 2

T.F.(h(x))=h^()= de -l'infini à + -l'infini de h(x).exp(-2ix).dx

Ensuite je multiplie par 2 0 et je sort ce terme de l'intégrale
Puis je sais que rect()=1 pour (-1/2)<<1/2, 0 ailleurs

d'où les bornes de l'intégrale : de (-1/2) à 1/2 de exp(-2ix).dx
d'où : la réponse impulsionnelle, h(t)=|20|.sinc(2x0)

Posté par
gigi7ore : Convolutions 12-11-14 à 18:26

2) a) Graphique

Convolutions

Posté par
Aragornre : Convolutions 12-11-14 à 21:18

OK pour la convolution.
Pour le message "posté le 12-11-14 à 18:06", c'est censé répondre à la question 3d partie B ?
Le filtre est exactement le même que dans la partie A donc la fonction de transfert est la même que la 1d partie A.
(h(t) = rect(t/T + 1/2) - rect(t/T - 1/2), T > 0 )

Posté par
gigi7ore : Convolutions 12-11-14 à 21:30

Si c'était possible d'avoir la correction des questions suivantes afin que je puisse comparer si ce que j'ai et juste et au cas contraire utiliser votre démarche afin d'arriver à votre résultat:

Citation :
Partie B :

3)  Filtre dérivateur

On modélise la réponse impulsionnelle de ce filtre par :
h(t) = rect(t/T + 1/2) - rect(t/T - 1/2), T > 0


a) Représenter graphiquement h(t), en indiquant les abscisses importantes.  

c)  Soit un signal défini  par : f(t)=y0 rect(t/6T)
                   .
Donner graphiquement le résultat de la convolution de ce signal par la réponse impulsionnelle du filtre.

d) Calculer la fonction de transfert de ce filtre.


Partie C :

1)  On désire réaliser un filtre passe-bas parfait de fonction de transfert h^(v)=rect(v/2v0), avec  v0>0.
- Calculer sa réponse impulsionelle.
- Ce filtre est-il réalisable en temps réel ? Justifier votre réponse.

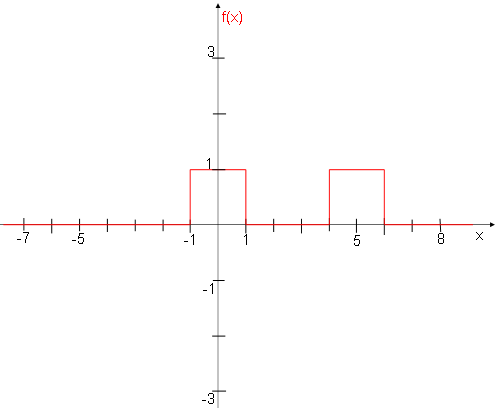
2) a)  Représenter graphiquement en graduant l'axe des abscisses et l'axe des ordonnées la fonction :
f(x) = rect(x/2) + rect((x-5)/2)

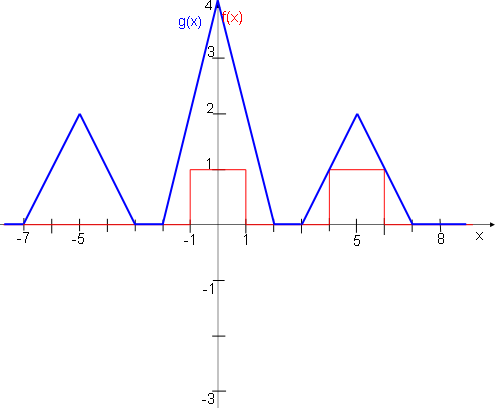
b) Calculer et représenter graphiquement, en graduant l'axe des abscisses et l'axe des ordonnées, la fonction g(x) = f(x) * f(-x ). Vérifiez votre résultat : que pouvez vous dire sur la parité de g(x) ? Pourquoi ?


Merci d'avance

Posté par
gigi7ore : Convolutions 12-11-14 à 22:21

Ok merci
Et pour :

Citation :
Partie C :

1)  On désire réaliser un filtre passe-bas parfait de fonction de transfert h^(v)=rect(v/2v0), avec  v0>0.
- Calculer sa réponse impulsionelle.
- Ce filtre est-il réalisable en temps réel ? Justifier votre réponse.

2) a)  Représenter graphiquement en graduant l'axe des abscisses et l'axe des ordonnées la fonction :
f(x) = rect(x/2) + rect((x-5)/2)

b) Calculer et représenter graphiquement, en graduant l'axe des abscisses et l'axe des ordonnées, la fonction g(x) = f(x) * f(-x ). Vérifiez votre résultat : que pouvez vous dire sur la parité de g(x) ? Pourquoi ?

Posté par
Aragornre : Convolutions 12-11-14 à 23:54

Partie C
1)   \Large h(t)\,=\,\int_{-\infty}^{+\infty}H(\nu)\,e^{2i\pi\nu t}\,d\nu\,=\,\int_{-\nu_0}^{+\nu_0}\,e^{2i\pi\nu t}\,d\nu\,=\,\left[\frac{e^{2i\pi\nu t}}{2i\pi t}\right]_{-\nu_0}^{+\nu_0}\,=\,\frac{e^{2i\pi\nu_0 t}\,-\,e^{-2i\pi\nu_0 t}}{2i\pi t}\,=\,\frac{sin(2\pi\nu_0 t)}{\pi t}\,=\,2\nu_0\,\frac{sin(2\pi\nu_0 t)}{2\pi\nu_0 t}

h(t)0 pour t < 0 ==> filtre non causal.

La suite dans peu de temps...

Posté par
Aragornre : Convolutions 13-11-14 à 00:18

2a)

Convolutions

Posté par
gigi7ore : Convolutions 13-11-14 à 06:41

Merci pour pour vos réponses
Et pour ce qui est de la question c) je dois dire que le produit de convolution donne une fonction g(x) paire ?

Posté par
Aragornre : Convolutions 13-11-14 à 11:07

3c
g(x) est l'autocorrélation de f(x). L'autocorrélation est réelle, paire et maximum en 0 .
g(x) = f(x) * f(-x)
g(-x) = f(-x) * f(x)
Le produit de convolution est commutatif : f(x) * f(-x) = f(-x) * f(x).
Donc  g(x) = g(-x) . La fonction g(x) est donc paire (ce qui est normal puisque c'est une fonction d'autocorrélation).

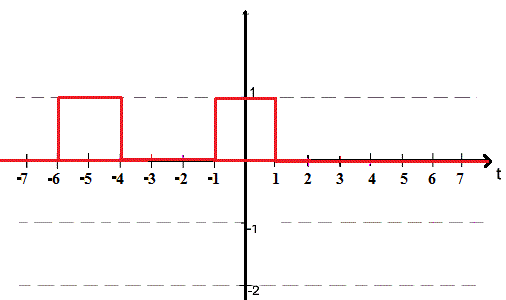
Convolutions

Posté par
Aragornre : Convolutions 13-11-14 à 11:15

Définition de l'autocorrélation
\Large R_X(t)\,=\,x(t)*x^*(-t)\,=\,\int_{-\infty}^{+\infty}x(\tau)\,x^*(\tau-t)\,d\tau
x^*  désigne le conjugué mais, ici, f(x)  est réelle donc  f^*(x)\,=\,f(x)
Donc  \Large g(x)\,=\,\int_{-\infty}^{+\infty}f(\tau)\,f(\tau-x)\,d\tau

Posté par
gigi7ore : Convolutions 13-11-14 à 12:46

Ok merci bien

En tout cas merci infiniment pour votre aide ainsi que vos explications claires

Posté par
Aragornre : Convolutions 13-11-14 à 14:32

A une prochaine fois...

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !