Niveau école ingénieur

Contraintes dans une couronne

Posté par
Nerf 17-11-25 à 17:50

Bonjour,
Considérons une couronne de rayons intérieur et extérieur respectifs a et b et d'épaisseur h très faible (approximation plaque).

1er cas : La couronne est en rotation uniforme autour de son axe. Ainsi, en se plaçant dans le référentiel tournant, c'est comme si une force volumique centrifuge était appliquée en chaque point de la plaque. L'objectif est d'établir l'étude dynamique de la couronne. Dans le corrigé, il est indiqué que la contrainte de cisaillement $\sigma _{ r \theta}$ est nulle à cause de la symétrie géométrique.

2e cas : La couronne étant au repos, on applique un couple de moments repartis sur ses surfaces extérieures dans le plan perpendiculaire à l'axe. Le corrigé mentionne que la seule contrainte non nulle est la composante $\sigma _{r \theta }$ , $\sigma _{rr}$ et $\sigma _{\theta \theta}$ étant nulles.

Ces contraintes sont définies par rapport aux facettes que je semble avoir compris mathématiquement mais pas physiquement. Face à un exercice, j'ai du mal à établir une analyse pour prédire et garder uniquement les contraintes pertinentes. J'aimerais svp que vous m'aidiez car je ne comprends pas leurs justifications. Je voudrais aussi que vous m'expliquer physiquement comment agissent ces contraintes dans le repère cylindre (suivant les directions rr, rz, $\theta z$ ... aussi) et ce que ça implique dans le cas où chacune est non nulle. Je vous remercie d'avance.

Posté par re : Contraintes dans une couronne 18-11-25 à 05:37

Bonjour,

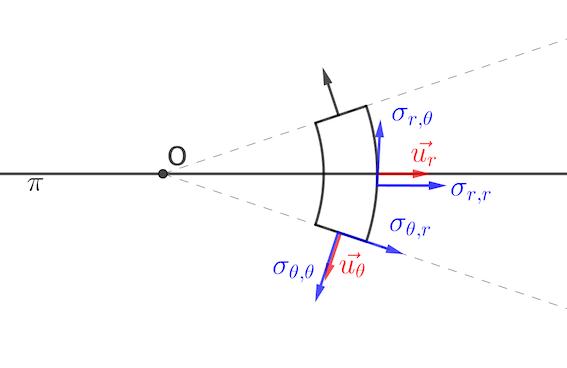
J'ai indiqué les diverses contraintes sur le schéma ci-dessous.
(je n'ai peut-être pas respecté les conventions de signe).

Si on fait des raisonnements analogues à ceux des vecteurs (principe de Curie), cela donne (mais il y a sans doute des raisonnements plus évolués pour les tenseurs) :

Si on fait une symétrie par rapport au plan π, dans le 1er cas, pas de changement, dans le deuxième changement de signe.

1er cas : la symétrie conserve σrr, mais change le signe de σrθ qui doit être inchangé, il est donc nul.

2eme cas : la symétrie conserve σrr, qui doit changer de signe, il est donc nul. La symétrie envoie σθθ sur l'autre face en changeant de direction, mais la direction de la normale a aussi changé, donc au total la symétrie conserve σθθ qui est donc nul.

Contraintes dans une couronne

Posté par re : Contraintes dans une couronne 19-11-25 à 11:09

Bonjour,
Je vous remercie !

Posté par re : Contraintes dans une couronne 22-11-25 à 08:21

Bonjour,
Je me rends compte que je n'ai pas bien compris la justification de $\sigma \theta \theta$ . Pouvez-vous svp mieux développer ? De plus, $\sigma \theta r$ du cas est symétrique par rapport au plan. Pourquoi n'est-il pas nul ?

Posté par re : Contraintes dans une couronne 22-11-25 à 11:54

Bonjour,

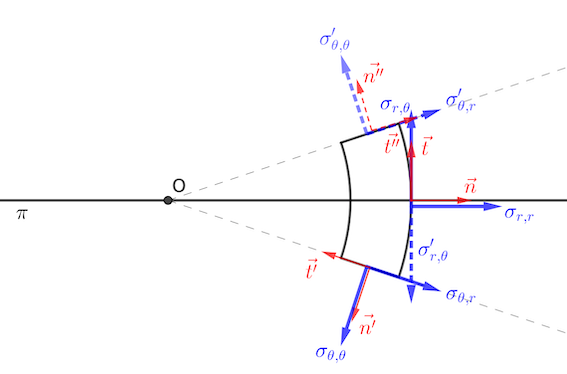
J'ai précisé le schéma : indiqué en pointillé les symétries, en bleu les vecteurs contraintes, en rouge les normales et tangentes pour projeter les dits vecteurs.

La symétrie par rapport à π transforme le vecteur $\sigma_{\theta,\theta}$ en $\sigma'_{\theta,\theta}$ , en même temps que le vecteur unitaire normal à la surface passe de $\vv{n'}$ à $\vv{n''}$ , au vu du dessin la composante $\sigma_{\theta,\theta}$ , projection du vecteur sur la normale est donc inchangé.
Donc cohérent avec le cas 1 et contradictoire avec le 2.

La symétrie par rapport à π transforme le vecteur $\sigma_{\theta,r}$ en $\sigma'_{\theta,r}$ , en même temps que le vecteur unitaire normal à la surface passe de $\vv{t'}$ à $\vv{t''}$ , au vu du dessin la composante $\sigma'_{\theta,r}$ , projection du vecteur sur la normale change donc de signe.
Donc cohérent avec le cas 2 et contradictoire avec le 1.

Et cohérent avec le comportement de $\sigma_{r,\theta}$ puisque le tenseur est symétrique.

J'ai l'impression qu'il y a des méli-mélo d'images au niveau du site.
Je reposterai l'image si nécessaire.

Contraintes dans une couronne