Inscription / Connexion Nouveau Sujet
conservation du moment cinétique
Bonsoir, je suis bloqué sur un exos, voici l'énoncé et le schéma que je joins en photo :
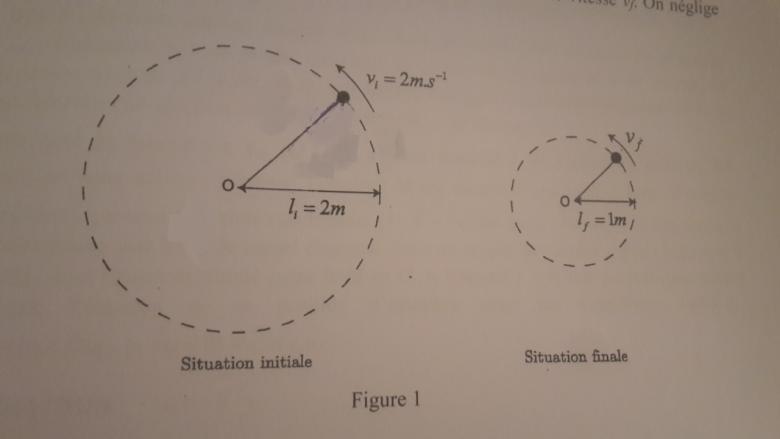
Soit un point matériel de masse m = 300g accrochée à un fil de masse négligeable et de longueur initial li=2 m . Dans un premier temps la masse est en rotation uniforme autour d'un point O. La vitesse linéaire est de vi=2m/s. Dans un deuxième temps, on réduit son rayon jusqu'à lf=1m ; la masse est alors animée d'une vitesse vf. On néglige les frottements.
Donner la norme du moment cinétique, puis la vitesse finale.
Alors si j'ai bien compris, l'exo résume à montrer qu'il va y avoir conservation du moment cinétique entre les deux situations. Mais je n'arrive pas à le montrer rigoureusement. En exprimant l'accélération en coordonnée cylindrique, j'ai pu dire que la dérivée du moment cinétique par rapport au temps était : .
Seulement j'ai l'impression qu'il faudrait montrer que c'est la dérivée du moment cinétique par rapport au rayon qui est nulle, mais alors là je sais pas trop.
Bonjour
Le moment cinétique en un point est le moment vectoriel en ce point de la quantité de mouvement.
Le moment cinétique initial, calculé au point O dans le référentiel d'étude supposé galiléen, est ainsi :
où désigne la base polaire usuelle et où
est un vecteur unitaire perpendiculaire au plan de figure orienté vers le lecteur.
Dans ce référentiel galiléen, le théorème du moment cinétique appliqué au point O à la masse m s'écrit :
La dérivée par rapport au temps du vecteur moment cinétique est égal à chaque instant au moment en O de la résultante des forces appliquées à la masse m. On suppose que la masse ponctuelle glisse sans frottement sur une table horizontale (mobile auto-porté par exemple) de sorte que le poids est à chaque instant compensé par la réaction de la table. Dans ces conditions, la résultante des forces se réduit à la tension du fil :
Il y a bien conservation du moment cinétique au cours du temps :
N'hésite pas à poser d'autres questions si cela ne te parait pas clair !
Bah ça me parait plutot clair, enfin j'ai quand même une question : Pourquoi avec cet exo, on peut dire que le poid est compensé ?
L'énoncé parle de mouvement circulaire uniforme à l'état initial et à l'état final. Dans ces deux cas, la tension du fil est à chaque instant perpendiculaire au vecteur vitesse : sa puissance instantanée est à chaque instant nulle, cette force ne travaille pas, on ne lui attribue pas d'énergie potentielle ; cette force est sans influence sur la norme du vecteur vitesse. Imagine dans ces conditions que la trajectoire n'appartienne pas à un plan horizontal : les variations d'altitudes correspondraient à des variations d'énergie potentielle qui engendreraient, par conservation de l'énergie mécanique, des variations d'énergie cinétique donc des variations de la norme du vecteur vitesse. La trajectoire appartient donc à un plan horizontal et dans ce cas, il faut bien compenser le poids...
Attention : lors du raccourcissement du fil, la trajectoire n'est plus circulaire, la tension du fil travaille pour faire varier l'énergie cinétique de la masse m.


