Inscription / Connexion Nouveau Sujet
Conducteur munit d'une cavité
Bonjour,
Voilà le schéma exact de mon exercice tiré du site suivant: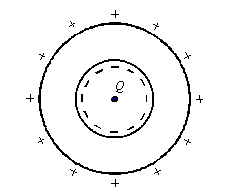
Je dois calculer le champ et le potentiel pour tout point de l'espace. Sachant que la cavité possédant une charge est de rayon R1 et la cavité plus le conducteur sont de rayon R2.
Dans ma correction on me dit que le champ E quand r<R1 en appliquant le théorème de gauss est égal à q/4*pi*epsillon0*r²
Mais pourquoi ce champ n'est il pas nul car la somme de l'ensemble des charges à l'intérieur de la cavité doit être nulle par définition .
Merci d'avance
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Et je salue prbebo  !
!
Bonsoir laselle,
tu vas te faire bientôt reprendre par le modérateur du forum, car ici les règles sont strictes : tu dois faire l'effort de recopier toi-même l'énoncé de ton exercice, au lieu de renvoyer à un site web. Il y a une charte de bonne conduite que tu peux lire ici (clique sur la maison) : ![]() [lien].
[lien].
Cela dit, si j'ai bien compris, il s'agit d'un conducteur comportant une cavité (sphérique en l'occurrence), et porté à un potentiel non nul, mais dont la charge globale est nulle (puisqu'il y a des charges sur la face interne de la cavité, donc forcément aussi sur la face externe de rayon R2). Dans ce cas, en tout point intérieur à la cavité (donc r < R1) le champ E est nul, puisque toutes les charges sont extérieures à la surface de Gauss (sphère de rayon r < r1). Celui qui t'a vendu ce corrigé n'est pas digne de ta confiance. A moins que j'aie mal interprété l'énoncé, que je t'engage à recopier ici.
bonjour
Merci de votre réponse 
Je tenais à dire que l'énoncé n'est pas sur le site que j'ai joint ...et que la question sur l'énoncé était dans mon post ... J'ai juste voulu ajouter un schéma qui était sur ce site... Il illustrait bien la problème de mon énoncé... Mais mon énoncé était différent...
Dsl si ça a prêté à confusion 
Bonjour laselle,
et bonjour coll  ! j'ai toujours plaisir à te retrouver au détour d'un exercice, et si je ne suis pas très bavard sur ma messagerie quand tu m'envoies un courriel, je sais que tu ne m'en tiens pas grief (d'ailleurs quelqu'un ici te surnomme cool... il y a sûrement une bonne raison
! j'ai toujours plaisir à te retrouver au détour d'un exercice, et si je ne suis pas très bavard sur ma messagerie quand tu m'envoies un courriel, je sais que tu ne m'en tiens pas grief (d'ailleurs quelqu'un ici te surnomme cool... il y a sûrement une bonne raison  !).
!).
Bon, laselle, on revient à nos affaires :
"Je tenais à dire que l'énoncé n'est pas sur le site que j'ai joint" : en effet, l'énoncé n'est nulle part.
"la question sur l'énoncé était dans mon post" : c'est vrai mais en même temps, demander le calcul du champ et du potentiel, c'est plutôt classique dans un exercice d'électrostatique...
"Il illustrait bien la problème de mon énoncé" : je ne trouve pas, car il n'y a aucune information concernant l'état électrique du conducteur avant qu'on n'y introduise la charge ponctuelle Q. D'ailleurs sur le schéma cette charge est tellement ponctuelle que je l'ai confondue avec le centre des deux sphères !
Voici comment on aurait pu poser cet énoncé :
Soit un conducteur sphérique dans lequel on a pratiqué une cavité également sphérique ; le rayon de cette cavité est R1, celui du conducteur R2.
Le conducteur étant initialement neutre, on introduit à l'intérieur de la cavité une charge ponctuelle Q positive, maintenue fixe au centre O des deux surfaces sphériques.
Calculer le champ électrostatique E(r) et le potentiel V(r) en tout point de l'espace.
L'info "conducteur initialement neutre" est primordiale, car puisqu'il est isolé sa charge totale restera nulle, même si les charges qu'il contient vont changer de place.
L'info "charge Q maintenue fixe" aussi, car si elle est capable de se déplacer elle quittera le centre O pour aller sur la face externe du conducteur.
Comme tu as déjà le corrigé de cet exercice, je ne vais pas détailler les calculs mais simplement te donner la marche à suivre ainsi que les résultats :
a) Symétrie : sphérique, donc la surface de Gauss ( ) est une sphère de centre O et de rayon r. Le flux sortant de cette sphère est
) est une sphère de centre O et de rayon r. Le flux sortant de cette sphère est  = 4
= 4 r2.E(r).
r2.E(r).
b) L'origine des potentiels peut être prise à l'infini (car pas de charges à l'infini). Donc il faut commencer par faire l'étude de E et de V à l'extérieur du conducteur (r > R2) et "avancer à reculons" (diminuer r pour entrer progressivement dans le système).
c) r > R2 :  enferme une charge Q (charge globale nulle sur le conducteur), d'où E(r) = Q/(4
enferme une charge Q (charge globale nulle sur le conducteur), d'où E(r) = Q/(4
 0r2), V(r) = Q/(4
0r2), V(r) = Q/(4
 0r).
0r).
d) R1 < r < R2 : si on appelle Q' la charge portée par la face interne du conducteur (sphère R1), la charge enfermée dans  est Qint = Q + Q'. Mais on est dans la partie métallique du conducteur, donc le champ y est nul en tout point. Le théorème de Gauss fonctionne donc ici "à l'envers", càd que connaissant E on en déduit Qint (souvent c'est l'inverse). Qint = 0, ce qui implique Q' = -Q. Comme la charge Q est choisie positive, la face interne du conducteur porte la charge négative -Q répartie uniformément sur toute la surface sphérique de rayon R1 (et par conséquence, la face externe de rayon R2 porte la charge +Q également répartie uniformément).
est Qint = Q + Q'. Mais on est dans la partie métallique du conducteur, donc le champ y est nul en tout point. Le théorème de Gauss fonctionne donc ici "à l'envers", càd que connaissant E on en déduit Qint (souvent c'est l'inverse). Qint = 0, ce qui implique Q' = -Q. Comme la charge Q est choisie positive, la face interne du conducteur porte la charge négative -Q répartie uniformément sur toute la surface sphérique de rayon R1 (et par conséquence, la face externe de rayon R2 porte la charge +Q également répartie uniformément).
Dans cette région : E(r) = 0, V(r) = constante = V0 : tout le volume du conducteur est au même potentiel, dont la valeur est obtenue par continuité avec l'extérieur. On trouve V0 = Q/(4
 0R2).
0R2).
e) r < R1 :  enferme la charge ponctuelle Q, on retrouve E(r) = Q/(4
enferme la charge ponctuelle Q, on retrouve E(r) = Q/(4
 0r2) comme à l'extérieur du conducteur. On en déduit V(r) = Q/(4
0r2) comme à l'extérieur du conducteur. On en déduit V(r) = Q/(4
 0r) + K, la constante K étant ajustée pour assurer la continuité du potentiel. Pour r = R1 on doit retrouver V0, ce qui fournit K = Q/(4
0r) + K, la constante K étant ajustée pour assurer la continuité du potentiel. Pour r = R1 on doit retrouver V0, ce qui fournit K = Q/(4
 0).(1/R2 - 1/R1) (remarque : K est négative).
0).(1/R2 - 1/R1) (remarque : K est négative).
Finalement, V(r) = Q/(4
 0).(1/r -1/R1 + 1/R2).
0).(1/r -1/R1 + 1/R2).
Bilan des courses : Le conducteur était initialement dépourvu d'énergie (pas de charges, potentiel nul). La présence de la charge ponctuelle lui a communiqué une énergie électrostatique (We = (1/2).CV02 si tu connais cette relation). Cette énergie est égale, au signe près, au travail des forces appliquées aux charges électriques du conducteur pour les déplacer (les positives à l'extérieur, les négatives à l'intérieur).
Si on supprime la charge ponctuelle Q, le conducteur restitue intégralement cette énergie (les charges reprennent leur place initiale en effectuant cette fois un travail moteur), et son potentiel retombe à zéro.
Si tu as des questions, n'hésite pas.
Merci ... Je ferais plus attention la prochaine fois à mettre la totalité des questions ... Excusez moi ...
Encore merci de votre réponse 


