Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

condensateur hémisphérique

Posté par
Meg09 16-04-20 à 17:07

Bonjour,

Voici l'énoncé :
une sphère conductrice creuse de masse M, de rayon R est séparée de deux parties inégales par un plan horizontal : on obtient deux calottes sphériques inégales dont la base commune est un cercle de rayon r=Rsin\theta
La sphère est portée au potentiel V>0, puis isolée.

1)En supposant que le champ électrique est radial à la sphère et vaut E=\frac{\sigma }{2\varepsilon }(  est la distribution de charge de la sphère). Quelle est la valeur de V de la sphère ?
V=-\int E dr Et puisque E ne dépend pas de r, V = -E ?

2)Démontrer que la force élémentaire qui s'applique sur la calotte supérieure vaut : \vec{dF} = \frac{\sigma ^{2}}{2\varepsilon }\vec{N}dS
(N est le vecteur surface de la calotte shpérique supérieure dont une surface élémentaire est dS) Quelle est la force résultante pour l'ensemble de la surface de la calotte en fonction de \alpha ,\sigma ,\varepsilon  et dS ?
Pour la force élémentaire, je pensais m'appuyer sur la formule F=Eq et donc dF=dE * dq. Mais, je ne sais pas comment trouver dq ou dE.
Et pour la force résultante, je ne sais pas trop comment m'y prendre.

3) Montrer qu'en coordonnées sphériques dS=2r2sin()d
S=4r2. Je pensais partir de ce qu'il nous donne et calculer S=dS et trouver le même résultat. Mais, il y a surement une autre façon de le montrer

4) En supposant la calotte inférieure fixe, montrer que la force qui s'applique sur l'ensemble de la calotte supérieur est F=V2sin2().

5) Dans le cas où la coupure est faite dans un plan équatorial, pour quelle valeur de V y aura-t-il séparation de deux hémisphères ? (la sphèrea une masse M)

Pour les 2 dernières questions, j'ai du mal à comprendre.

J'aurais besoin d'aide pour réussir cette exercice.
Merci d'avance

Posté par
vanoisere : condensateur hémisphérique 16-04-20 à 17:15

Bonjour
Pourrais-tu expliquer ce que tu as réussi à faire et ce qui te bloque ? Plus facile de t'aider ensuite !

Posté par
vanoisere : condensateur hémisphérique 16-04-20 à 17:22

Pour la question 1 : l'énoncé n'est pas très clair : on demande l'expression de V sans préciser en fonction de quoi : en fonction de , R et o ?
En tout cas : un potentiel et une norme de vecteur champ sont deux grandeurs de natures différentes, elles ne peuvent être égale au signe près. C'est un peu comme si tu écrivait : L=-t avec L : longueur et t : temps....

Posté par
Meg09re : condensateur hémisphérique 16-04-20 à 17:38

Ah oui, je comprends. D'ailleurs, j'ai fait une erreur dans mon raisonnement : V=-Edr. Donc, V = -\frac{\sigma r}{2\varepsilon } ?
Et non, l'énoncé ne demande pas en fonction de quelle valeur

Posté par
vanoisere : condensateur hémisphérique 16-04-20 à 17:52

C'est déjà mieux au niveau de l'homogénéité mais ce n'est pas tout à fait cela. Le rappel du théorème de Coulomb donnant l'expression du vecteur champ au voisinage immédiat de la sphère, côté extérieur n'est vraiment utile que pour la question 2 et les suivantes. Il y a beaucoup plus simple pour le potentiel.
Quel est l'expression générale du potentiel créé en un point M de l'espace ? Tu en déduis sans calcul le potentiel au centre O de la sphère. Ensuite : tu as dû démontrer en cours qu'un conducteur chargé (creux ou pas) délimite un volume équipotentiel : le potentiel est le même en tout point de la surface de la sphère et en tout point à l'intérieur de la sphère. C'est pour cela qu'on demande le potentiel de la sphère sans préciser en quel point on le calcule. Ce potentiel est donc en particulier la valeur au centre.
Pour la deuxième question : commence par te poser la question : de quelle force exactement s'agit-il ? Il faut une réponse de la forme : force exercée par ... sur  ... C'est un peu subtil je le reconnais...

Posté par
Meg09re : condensateur hémisphérique 16-04-20 à 18:18

Au point M : V=\frac{Q}{4\pi \varepsilon r}
Au centre, r=0. Donc, V=0 ? Ca me semble bizarre.
C'est une force exercé par une charge sur la calotte supérieur de la sphère ?

Posté par
vanoisere : condensateur hémisphérique 16-04-20 à 18:37

Dans le cas général, le potentiel en un point M quelconque, si la charge élémentaire dq est centrée en P :

V_{(M)}=\frac{1}{4\pi\varepsilon_{o}}\iiint\frac{dq}{\Vert\overrightarrow{PM}\Vert}
Puisque la sphère constitue un volume équipotentiel, on peut calculer le potentiel au centre O. Dans ce cas , toutes les charges étant surfaciques, sont situées à la distance R de O. Le potentiel s'écrit donc :

V=\frac{Q}{4\pi\varepsilon_{o}R}
où R est le rayon de la sphère et Q la charge totale qui peut simplement s'exprimer en fonction de R et .
Cet énoncé est vraiment très mal posé.
La force dont il faut déterminer l'expression \vec{dF}=\frac{\sigma^{2}}{2\varepsilon}\vec{N}dS est la force exercée sur la charge dq=.dS par toutes les autres charges de la calotte sphérique, donc par la charge (Q-dq). Si on cherche à exprimer cette force sous la forme : \overrightarrow{dF}=\sigma.dS.\overrightarrow{E} , que représente le vecteur champ E (vecteur champ créé par quelles charges) ?

Posté par
Meg09re : condensateur hémisphérique 16-04-20 à 19:17

Ok et ici, =Q/(2r2) ?
Le vecteur E est créé par toutes les autres charges de la calotte supérieur. Ok, j'ai compris pour cette question.
Et la force résultante c'est dF multiplié par la surface de la calotte supérieur ?

Posté par
vanoisere : condensateur hémisphérique 16-04-20 à 20:01

Non !
Le rayon de la sphère est noté R ; la notation r est réservée à la distance d'un point quelconque M au centre O (voir coordonnées sphériques). Sachant que l'aire d'une sphère est S=4R2, tu obtiens :

V=\frac{Q}{4\pi\varepsilon_{o}R}=\frac{4\pi R^{2}.\sigma}{4\pi\varepsilon_{o}R}=\frac{\sigma.R}{\varepsilon_{o}}

Citation :
Le vecteur E est créé par toutes les autres charges de la calotte supérieur

C'est plus subtil que cela ! Imagine un petit élément de surface dS assimilable à un peit disque de rayon très faible. Il possède la charge dq=dS. Le vecteur champ E à prendre en compte est celui créé par toutes les autres charges présentes.
C'est l'expression de ce vecteur champ qui est fournie par l'anoncé car le vecteur champ créé par toutes les charges, y compris la charge dq, serait le double de celui indiqué par l'énoncé. Voilà bien des subtilités dont l'énoncé, tel que tu l'as copié, ne parle pas !

Posté par
Meg09re : condensateur hémisphérique 16-04-20 à 20:33

vanoise @ 16-04-2020 à 20:01

Non !
Le rayon de la sphère est noté R ; la notation r est réservée à la distance d'un point quelconque M au centre O (voir coordonnées sphériques). Sachant que l'aire d'une sphère est S=4R2, tu obtiens :
V=\frac{Q}{4\pi\varepsilon_{o}R}=\frac{4\pi R^{2}.\sigma}{4\pi\varepsilon_{o}R}=\frac{\sigma.R}{\varepsilon_{o}}

Ca voudrait dire que E=\frac{Q}{2*4\pi R^2 \varepsilon} ?
vanoise @ 16-04-2020 à 20:01

C'est plus subtil que cela ! Imagine un petit élément de surface dS assimilable à un peit disque de rayon très faible. Il possède la charge dq=dS. Le vecteur champ E à prendre en compte est celui créé par toutes les autres charges présentes.
C'est l'expression de ce vecteur champ qui est fournie par l'anoncé car le vecteur champ créé par toutes les charges, y compris la charge dq, serait le double de celui indiqué par l'énoncé. Voilà bien des subtilités dont l'énoncé, tel que tu l'as copié, ne parle pas !

Donc, le champ E de l'énoncé est celui créé seulement pas toutes les autres charges présentes, toutes sauf dq ?

Posté par
vanoisere : condensateur hémisphérique 16-04-20 à 23:08

Citation :
Ca voudrait dire que E=\frac{Q}{2*4\pi R^2 \varepsilon} ?

Oui mais il est plus simple de conserver l'expression en fonction de et o.  Il s'agit du vecteur champ créé par toutes les charges sauf dq, ce qui n'était pas précisé dans l'énoncé. C'est celui dont tu dois te servir pour démontrer l'expression de dF.
PS : tu vas peut-être penser que je me mêle de ce qui ne me regarde pas mais, tant pis, je me lance. En cette période, les étudiants travaillent souvent seuls sans toujours se rendre compte du niveau des exercices. Tu viens en quelques jours de passer d'un exercice simple sur le potentiel créé par quatre charges ponctuelles au plus difficile des exercices d'électrostatique, exercice suffisamment difficile pour avoir été retiré depuis quelques années des programmes de Math Spé. Et toi, tu postes au niveau Math Sup...
Pour vraiment bien comprendre cet exercice, il faut avoir compris le cours sur les conducteurs en équilibres électrostatiques, cours habituellement aux programmes des filières (bac+2). Au niveau (bac+1), on se limite habituellement aux problèmes de vecteurs champ et de potentiels créés par diverses distributions continues de charges :  tige électrisée, disque électrisée, boule chargée...

Posté par
Meg09re : condensateur hémisphérique 17-04-20 à 10:58

Bonjour,

Je ne savais pas que c'était un exercice type BAC+2, je ne suis qu'en BAC+1 ; mais c'est un des exercices que nous a donné notre prof de physique à faire pendant la semaine de vacances. Je n'ai pas vraiment d'autres choix que de le faire même si j'avoue avoir beaucoup plus de mal avec cet exercice que les autres. Concernant le niveau, je ne sais pas réellement la différence entre Maths Sup et Maths Spé dans le supérieur, je suis en prépa intégré dans une école d'ingénieur.

Sinon, pour l'exercice j'ai réussi à faire la 1 et la 2 sauf pour la force résultante, il faut bien multiplier dF par la surface de la calotte  supérieur ? Si c'est le cas, j'ai du mal à exprimer cette force avec .

Pour la 3) ça marche si je montre que ds (qu'il nous donne) est égal à 4r2 ?

Pour la 4) à mon avis, il me faudrait la force résultante pour pouvoir ensuite faire l'intégrale double de cette force.

Pour la 5) je n'ai vraiment aucune idée

Posté par
vanoisere : condensateur hémisphérique 17-04-20 à 12:12

À tout ce que j'ai écrit dans mon message précédent, s'ajoute le fait que cet exercice est très mal conçu (compétence de ton professeur...). Les notations sont parfois incohérentes.
Exemple 1 : désigne une des trois coordonnées sphériques. La calotte sphérique doit donc être caractérisée par la valeur maximale de cet angle qu'il ne faut pas noter mais, par exemple 1. Sinon, le calcul intégral va t'amener à noter à la fois la variable d'intégration et la borne supérieure  de l'intégrale. Qu'en penserait ton professeur de mathématiques ? Le rayon de la calotte sphérique est alors R1=R.sin(1)...
Exemple 2 : le dS de la formule \vec{dF}=\frac{\sigma^{2}}{2\varepsilon}\vec{N}dS n'a pas la même signification que le dS de la relation : dS=2R2sin().d.
En plus, la deuxième formule fournie est fausse...
Dans le premier cas, dS=R2sin().d.d : petit élément de surface de la calotte sphérique.
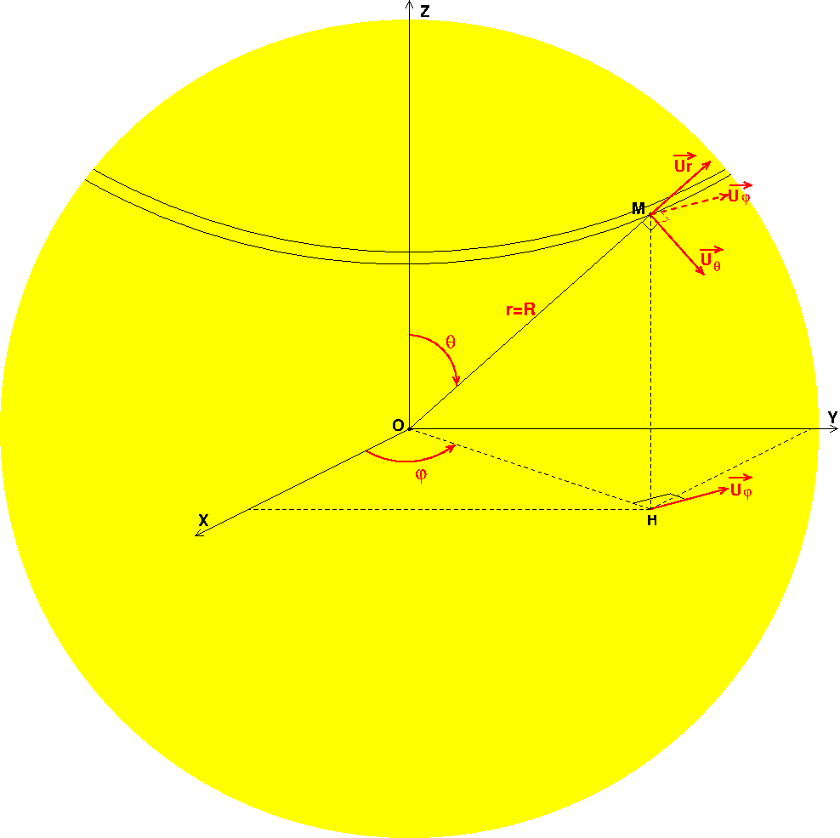
Dans le second cas, il s'agit de l'aire de la couronne d'épaisseur R.d de rayon R.sin(). (la partie avant de cette calotte est représentée sur le schéma ci-dessous). Il serait préférable de la noter dS' par exemple : dS'=2R2sin().d. Le schéma ci-dessous pourras peut-être t'aider. Le vecteur unitaire \vec{u_r} correspond au vecteur \vec N de ton énoncé.
Ensuite : considère un petit élément de surface entourant le point M ; il est soumis à la force \vec{dF}=\frac{\sigma^{2}}{2\varepsilon}\vec{N}dS. Considère maintenant le point M', symétrique de M par rapport à l'axe (Oz), entouré d'un élément de surface de même aire dS. Il est soumis à la force \vec{dF'}=\frac{\sigma^{2}}{2\varepsilon}\vec{N'}dS. Pour des raisons de symétrie, les composantes des forces suivant (Oz) vont s'ajouter alors que les autres composantes font s'annuler. Cela étant vrai pour tout couple de points {M,M'}, on peut affirmer que la résultante des forces élémentaires sera orientée suivant z et aura pour norme la somme des composantes de dF suivant z ; tu vas donc être amenée à faire la somme des :
dF.cos()...
Je te laisse réfléchir à tout cela...

condensateur hémisphérique

Posté par
Meg09re : condensateur hémisphérique 17-04-20 à 13:03

Je vous ai mis ci-dessous les schémas que j'ai.
Mon correspondrait à votre ? Mais, dans ces cas là, à quoi correspond mon sur mon 1e schéma ? Je vous avoue que j'arrive pas à comprendre réellement le schéma de mon énoncé.
serait l'angle maximal et un angle quelconque entre 0 et ?

Dans votre exemple, le force résultante serait 2dFcos ? (si j'ai bien compris)

condensateur hémisphérique

condensateur hémisphérique

Posté par
vanoisere : condensateur hémisphérique 17-04-20 à 14:07

Tu aurais dû scanner ces schémas dès le début... Les notations de ton professeur retrouvent leur cohérence même s'il ne s'agit pas des notations habituellement utilisées.
La coordonnée sphérique de mes messages et de mon schéma est notée dans ton énoncé.
Ce que j'ai noté 1 est noté dans ton énoncé. Cependant, l'aire de la couronne élémentaire s'écrit avec tes notations :
dS'=2R2.sin().d. (pas de r2 comme dans ton énoncé).
Si ces notations sont imposées par l'énoncé, utilise-les. Sinon : autant choisir les notations les plus habituelles...

Citation :
Dans votre exemple, le force résultante serait 2dFcos() ? (si j'ai bien compris)

ou 2dF.cos() avec tes notations. Oui si on s'intéresse aux deux éléments de surface centrés en M et en M'. Il est plus simple de juste remarquer que les composantes suivant (Oz) s'ajoutent alors que les autres composantes se compensent deux à deux par raison de symétrie.
Peux-tu maintenant exprimer la composante dF'z de la force exercée sur la couronne élémentaire ? Il suffit ensuite d'intégrer sur la totalité de la calotte.

Posté par
Meg09re : condensateur hémisphérique 17-04-20 à 14:38

vanoise @ 17-04-2020 à 14:07

Tu aurais dû scanner ces schémas dès le début...
Je suis désolée, avant que vous mettiez une image, je ne savais pas qu'on pouvait en mettre une.
vanoise @ 17-04-2020 à 14:07

Peux-tu maintenant exprimer la composante dF'z de la force exercée sur la couronne élémentaire ? Il suffit ensuite d'intégrer sur la totalité de la calotte.

dF'z = \frac{\sigma ^2}{2\varepsilon }\vec{N'_{z}}ds ?

Posté par
vanoisere : condensateur hémisphérique 17-04-20 à 15:09

Je reprends les notations de ton schéma. La force dF' exercée sur la couronne élémentaire est colinéaire à Oz.

\overrightarrow{dF'}=\frac{\sigma^{2}}{2\varepsilon_{o}}\cdot\cos\left(\alpha\right).dS'.\overrightarrow{u_{z}}=\frac{\sigma^{2}}{2\varepsilon_{o}}\cdot\cos\left(\alpha\right).2\pi.R^{2}.\sin\left(\alpha\right).d\alpha

La force exercée sur les charges de la calotte par les autres charges de la sphère a pour vecteur :

\overrightarrow{F'}=F'.\overrightarrow{u_{z}} avec :

F'=\frac{\pi.R^{2}.\sigma^{2}}{\varepsilon_{o}}\cdot\int_{0}^{\theta}\cos\left(\alpha\right).\sin\left(\alpha\right).d\alpha

Je te laisse terminer. Le plus dur est fait (je ne dirai pas par qui !).

Posté par
Meg09re : condensateur hémisphérique 17-04-20 à 15:30

Pour la force F, j'avais compris qu'il fallait faire l'intégrale de dF. Mais, la force résultante, ce n'est pas la somme de tous les dF ?
Sinon, pour la question 3 et 4 je pense savoir comment faire.
Il me reste que la question 5, je n'ai pas compris la question.

Posté par
vanoisere : condensateur hémisphérique 17-04-20 à 15:40

Faire la somme des dF : ce n'est pas intégrer ????
Question 5 : encore une question très mal posée (une de plus !). Il faut je pense imaginer la demie sphère inférieure posée sur un support isolant. On pose alors la demie sphère supérieure sur la demie sphère inférieure de façon à obtenir une sphère. On charge alors l'ensemble en le portant au potentiel V par rapport à la terre à l'aide d'une machine électrostatique. Les deux demies sphères portant des charges de même signe, tendent à se repousser. La demie sphère inférieure exerce sur la demie sphère supérieure la force verticale ascendante F' (valeur pour =/2). La demie sphère supérieure va décoller dès que F' deviendra supérieure au poids de la demie sphère M.g/2...

Posté par
Meg09re : condensateur hémisphérique 17-04-20 à 16:18

et donc résoudre l'inégalité F>Mg/2 avec =/2 ?

Posté par
vanoisere : condensateur hémisphérique 17-04-20 à 16:57

C'est bien cela. Il faut démontrer avant : F=\pi.\varepsilon_{o}.V^{2}.\sin^{2}\left(\theta\right) mais je t'ai fourni la méthode de calcul.

Posté par
Meg09re : condensateur hémisphérique 17-04-20 à 17:03

Oui, j'ai réussi. Je vous remercie encore pour votre aide et votre temps consacré pour moi.

Posté par
gbm Webmasterre : condensateur hémisphérique 17-04-20 à 19:02

Qu'est-ce que ce nouveau délire de poster un exercice et de se désinscrire ensuite ?

Posté par
keysersozere : condensateur hémisphérique 20-04-20 à 21:41

Bonsoir,
Je voulais vous demander si vous avez un livre, un site ou même une chaîne Youtube à me recommencer pour comprendre toute cette partie en physique s'il vous plait.

Posté par
vanoisere : condensateur hémisphérique 20-04-20 à 22:56

Bonsoir
Difficile de te conseiller efficacement sans connaître ton niveau...
Voici un premier document assez détaillé de niveau bac+1 sur les bases de l'électrostatique :

puis quelque chose d'un peu plus difficile sur le conducteur en équilibre électrostatique :


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !