Inscription / Connexion Nouveau Sujet
Condensateur en régime transitoire...
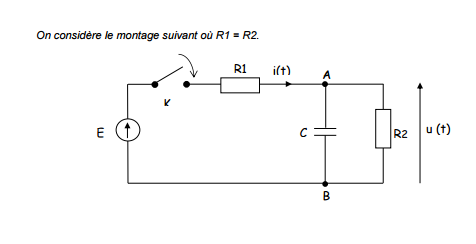
Bonsoir à tous, ayant un exercice à faire, celui-ci me pose problème. Mon problème est que je ne sais pas comment faire sachant qu'en TD, on a vu que des circuits avec 1 resistance. Voici l'énoncé :
1. Déterminer l'équation de u(t) lorsque l'on ferme l'interrupteur K et donner la valeur
maximale de u(t).
2. En déduire l'expression de la constante de temps lors de la charge du condensateur.
--> Lorsque C est pleinement chargé on ouvre K.
3. Déterminer l'équation de u(t).
4. En déduire l'expression de la constante de temps lors de la décharge du
condensateur.
---> On considère un circuit RL série alimenté par une tension continue E.
5. Faire un schéma faisant apparaitre E, R, L et i.
6. Donner l'expression du courant i(t) lors de la mise sous tension du circuit et donner
l'expression de la constante de temps.
7. En déduire l'expression de la tension aux bornes de la bobine.
Bonjour
La méthode générale pour établir l'équation différentielle consiste à écrire la loi des noeuds puis à exprimer chaque intensité en fonction de E , u, du/dt, C, R1, R2.
Pour résoudre l'équation différentielle, tu devras considérer qu'un condensateur assure la continuité de la tension à ses bornes.
Je te laisse réfléchir et proposer une solution. Cela sera plus efficace qu'un simple corrigé pas nécessairement adapté à ton niveau.
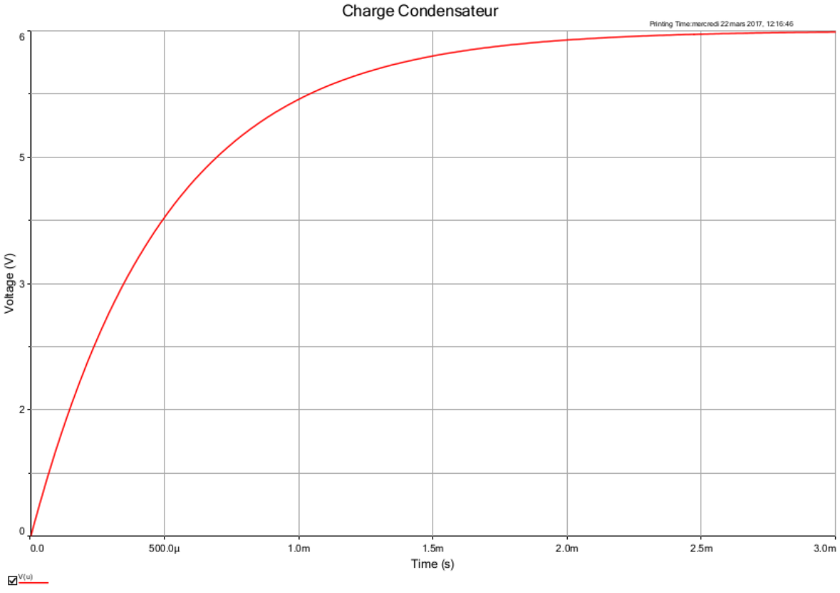
Pour t'aider un peu et te permettre de t'autocorriger, voici une simulation du montage que tu as posté en choisissant : E = 12V ; R1=R2=10k . Compare la valeur asymptotique de u à la valeur de E ; tu peux aussi évaluer la constante de temps et la comparer à la valeur théorique que tu as obtenue.
. Compare la valeur asymptotique de u à la valeur de E ; tu peux aussi évaluer la constante de temps et la comparer à la valeur théorique que tu as obtenue.
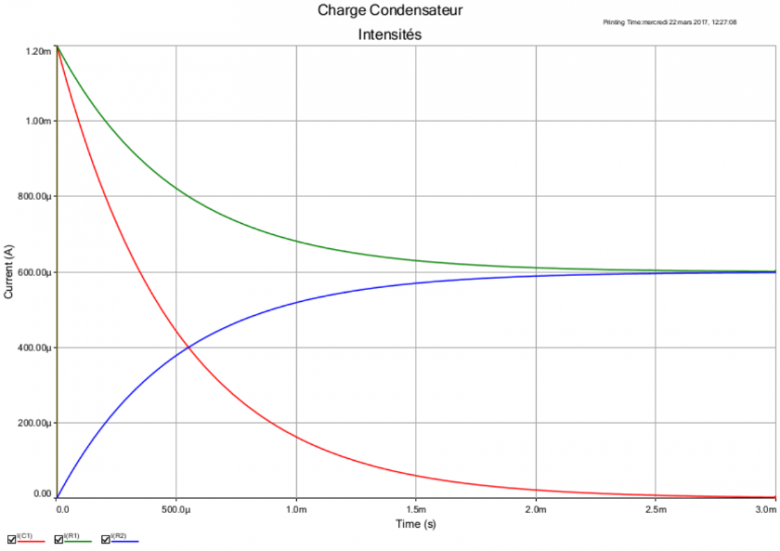
Je te postes aussi les courbes correspondant aux trois intensités ; cela pourra peut-être t'aider à mieux comprendre ce qui se passe.
Les autres questions sont des applications directes du cours.
Le problème est que je bloque pour simplifier le circuit car j'aurais dit que R1 et R2 sont en parallèle mais il y a un condensateur entre ces 2 résistances
Je t'ai indiquée la méthode: applique la loi des noeuds et exprime ensuite chaque intensité comme déjà expliqué.
Pour la loi des noeuds je propose :
E - UReq + Uc = 0 avec Req = R1 + R2 ?
Ou E - UR1 + Uc = 0 (car R1 = R2) ?
Tu confonds loi des noeuds et loi des mailles. Il faut écrire, en orientant correctement les dipoles:
i=i (C)+i (R2)
oú i (C) désigne l'intensité dans la branche du condensateur et oú i (R2) désigne l'intensité à travers R2...
Nous on faisait avec la loi des mailles pour établir l'équation différentielle. On sait de plus que I = dQ/dt = CdU/dt
On a : I = I(C) + I(R2)
I(C) = CdUc/dt et IR2 = U/R<=> dIR2/dt = 1/R2 dU/dt d'où
dQ/dt = CdUc/dt + 1/R2dU/dt ?
Nous on faisait avec la loi des mailles pour établir l'équation différentielle
Au lieu d'essayer de tenir compte de mes conseils, tu m'opposes la méthode de ton cours alors que, à en croire ton premier message, tu n'as étudié en cours que l'association en série d'un condensateur et d'une résistance... Pas très cohérent !
Enfin : vu le programme de l'enseignement secondaire en électricité, j'imagine bien que les choses ne sont pas faciles...
Loi des nœuds après avoir orienté les dipôles en convention récepteur (notations déjà expliquées) :
Loi d'Ohm appliquée à R2 :
Loi d'Ohm appliquée à R1 :
Propriété du condensateur vue en cours :
On reporte dans l'expression de la loi des nœuds :
Mise au même dénominateur et regroupement des termes dépendant de u :
Division de tous les termes par R1.R2.C :
Cette équation différentielle du premier ordre est analogue( pas identique) à celle vue en cours. Tu peux l'écrire sous la forme :
où
Tu as posté ton dernier message pendant que j'écrivais le mien ! Tu étais sur la bonne voie avec une erreur sur la loi d'Ohm concernant R1 : tu n'avais pas vu que la tension à ses bornes est (E-u), la résistance étant orientée en convention récepteur.
C'est une équation différentielle du 1er ordre linéaire et inhomogene :
Solution homogène :
U= Ke^-t/
Solution particulière :
U/ = cst -> du/dt = 0 d'où :
= cst -> du/dt = 0 d'où :
U= E*R2/R1+R2
Solution générale :
U(t) = Ke^-t/ + E*R2/R1+R2. Il faut déterminer K avec les CI : (U(0)= 0 ->
+ E*R2/R1+R2. Il faut déterminer K avec les CI : (U(0)= 0 ->
K = -E*R2/R1+R2
D'où U(t) = E*R2/(R1+R2)
*(1-e^-t/ )
)
Après avoir résolu le problème (et compris) comme indiqué par vanoise ...
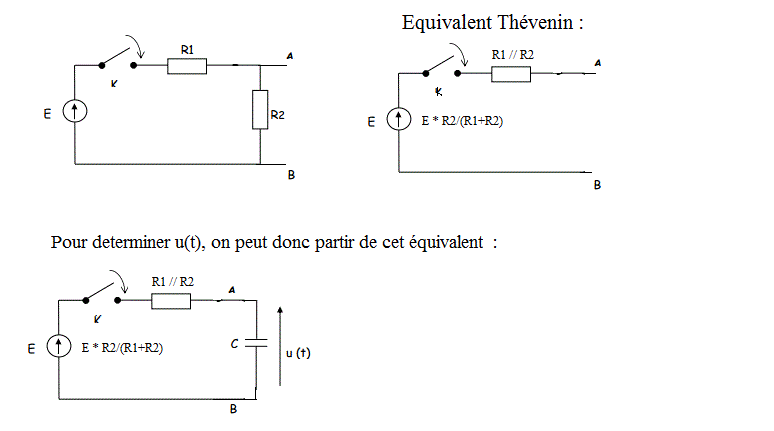
On peut aussi le faire par une autre approche (Equivalent Thévenin) qui devrait être connue en "Licence" :
Pour la charge :
...
Sauf distraction 
Oui... enfin pas tout à fait.
Tu avais écrit :
Le problème est que je bloque pour simplifier le circuit car j'aurais dit que R1 et R2 sont en parallèle mais il y a un condensateur entre ces 2 résistances
Si on maîtrise bien les équivalents Thévenin, on arrive au schéma simplifié que j'ai donné, mais cela doit être compris, ce qui ne semblait pas être ton cas avec ce que tu avais écrit ci-dessus.
Il n'empêche que l'approche en utilisant les lois des mailles et des noeuds doit aussi être parfaitement maîtrisée.

Ce que j'avais fait au début...
Oui... enfin pas tout à fait.
Je trouve JP extrêmement "gentil" avec cercus qui fait preuve ici d'une totale mauvaise foi !
Il me semble totalement impossible que quelqu'un, incapable de faire la différence entre la loi des nœuds et la loi des mailles (voir son message du 22-03-17 à 21:56), puisse maîtriser le théorème de Thévenin d'ailleurs disparu de la plupart des programmes à ce niveau d'enseignement !
Petite précision pour éviter tout malentendu : mes remarques précédentes ne m'empêchent pas de trouver l'intervention de JP intéressante : elle peut être utile à d'autres étudiants plus expérimentés fréquentant ce forum.
Plus de Thévenin en licence ?
Fichtre alors, tout fout le camp ... mais cela il y a longtemps qu'on le savait.

Bonsoir
@cercus : ton message du 23-03-17 à 07:59 est totalement correct !
@JP : en France,les théorèmes de Thévenin et Norton ont disparus des programmes bac(+1) bac(+2) ( y compris classes prépas) depuis très longtemps sauf dans quelques filières très spécialisées. En revanche, la transformation Thévenin-Norton perdure dans de nombreuses filières. La baisse des exigences (au moins sur le papier...) est nettement moins rapide dans d'autres pays francophones. Je ne suis d'ailleurs pas certains que tous les enseignants intervenant à l'université en licence sont au courant de la disparition totale de l'électricité des programme du second cycle de l'enseignement secondaire français !
La baisse des exigences (au moins sur le papier...) est nettement moins rapide dans d'autres pays francophones.
Ca ce n'est pas sûr du tout.

Reprenons :
1/ U(t) = Eth*(1 - e^-t/ ) Valeur max quand Ut = Eth
) Valeur max quand Ut = Eth
2/  = Rth*C
= Rth*C
3/ Ut - Urth = 0 <=> dUt/dt + Ut/ = 0
= 0
-> Résolution de cette equation :
Ut = Eth*e^^-t/
4/  = R2*C
= R2*C
Suite :
6/ On a UL = L*dI/dt et  = L/R
= L/R
Loi des mailles : E - UL - UR = 0
<=> dI/dt + I/ = (E/R)/
= (E/R)/
Solution de cette equation : I(t) = (E/R)*(1 - e^-t/ )
)
7/ U(t) = dI/dt => dI/dt = (E/( *R))*(e^-t/
*R))*(e^-t/ )
)
==> U(t) = (L/( *R)*(e^-t/
*R)*(e^-t/ ))
))


