Niveau autre

collision

Posté par
Alaa07 18-10-17 à 21:24

J'ai un exercice que j'arrive pas à le résoudre :
Une balle de baseball de 150 g arrive horizontalement avec une vitesse de 108 km / h. La force exercée par le bâton est illustrée dans le graphique ci-dessous. Quelle est la vitesse juste après la collision? la force du bâton sur la balle s' exerce à 45,0 degrés par rapport à la direction opposée à la vitesse initiale de la balle?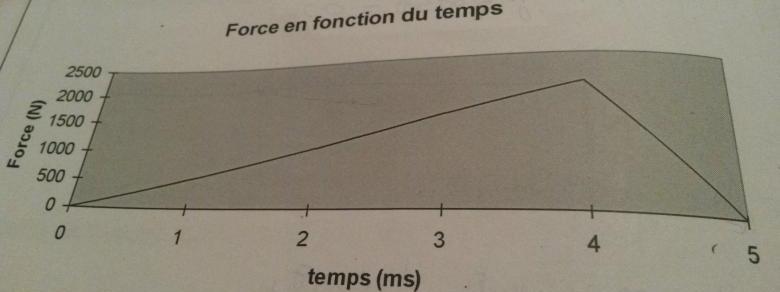

***Image recadrée***

Posté par re : collision 18-10-17 à 22:41

Bonsoir

En supposant le repère terrestre d'étude assimilable à un repère galiléen, tu peux appliquer à la balle la relation fondamentale de la dynamique :

$\overrightarrow{F_{(t)}}=m\cdot\frac{d\overrightarrow{V_{(t)}}}{dt}$

Si tu intègre cela entre les instants t1 et t2 correspondant au début et à la fin du contact avec le bâton, cela donne :

$\int_{t_{1}}^{t_{2}}\overrightarrow{F_{(t)}}\cdot dt=m\cdot\left(\overrightarrow{V_{(t_{2)}}}-\overrightarrow{V_{(t_{1})}}\right)$

Le poids de la balle étant de l'ordre de 1,5N, je pense que tu peux tout à fait négliger l'influence de ce poids devant celle de la force F(t) dont l'intensité atteint 2000N.

Il est possible de projeter la relation précédente sur deux axes, un horizontal et l'autre vertical.
Je te laisse réfléchir...

Posté par re : collision 18-10-17 à 22:55

J'ai comme l'impression d'avoir vu cet exercice quelque part, il n'y pas si longtemps ....

collision

Posté par re : collision 18-10-17 à 23:21

Bonsoir odbugt1 et merci de la remarque.
Effectivement... Le plus gênant est qu'apparemment l'auteur de la demande d'aide est le même...
Pas sympa : si Alaa07 n'a pas très bien compris l'aide fournie précédemment, pourquoi ne poursuit-il pas le même topic en demandant de l'aide supplémentaire au lieu de faire du multipost ?

Posté par re : collision 19-10-17 à 12:29

Bonjour
Il est tout à fait possible de résoudre très simplement cet exercice sans aller chercher Al Kashi. Il suffit de projeter la relation vectorielle que j'ai indiquée précédemment sur deux axes.
Je note :

$\overrightarrow{\triangle p}=\int_{t_{1}}^{t_{2}}\overrightarrow{F_{(t)}}\cdot dt$

Il s'agit d'un vecteur incliné de 45° par rapport à l'horizontale donc la norme est l'aire sous la courbe :

$\Delta p=\frac{1}{2}F_{max}\left(t_{2}-t_{1}\right)\approx0,5.2100.5.10^{-3}\approx5,25kg.m/s$

La projection de la relation sur l'axe des x, axe horizontal orienté dans la direction du vecteur v(t1) et en sens inverse conduit à :

$\Delta p.\cos\left(\frac{\pi}{4}\right)=m.\left(v_{x(t2)}-v_{x(t1)}\right)\quad avec\quad v_{x(t1)}=-30m/s$

On obtient ainsi $v_{x(t2)}$

La projection sur l'axe vertical ascendant conduit à :

$\Delta p.\sin\left(\frac{\pi}{4}\right)=m.v_{y(t2)}$

La vitesse de la balle juste après la collision est ainsi :

$\\ v_{(t2)}=\sqrt{v_{x(t2)}^{2}+v_{y(t2)}^{2}}$

L'angle $\alpha$ entre l'horizontale et ce vecteur vitesse vérifie :

$\tan\left(\alpha\right)=\frac{v_{y(t2)}}{v_{x(t2)}}$

Posté par re : collision 05-01-18 à 07:51

Bonjour,
j'ai pu remarquer que nous avions le même exercice à faire, je me demandais si il serait possible pour vous de m'envoyer une copie de votre démarche. je ne comprends pas bien les consignes des autres. je sais que c'est beaucoup demander.
merci

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

collision

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique