Inscription / Connexion Nouveau Sujet
Coefficients de dilatations thermodynamiques
Bonjour à tous,
J'ai des problèmes pour une question d'un exercice :
SUJET
1°) Coefficient de dilatation isobare α - Coefficient de compressibilité isotherme χT
Soit un liquide décrit par une équation d'état V = f(P,T) , V, P et T étant des variables d'état.
a) Ecrire dV en fonction de dP et dT. Donner les définitions des coefficients α et χT. Quelles sont leurs unités ?
Remplacer dans dV.
b) En intégrant successivement α et χT , donner la forme de cette équation V = f(P,T). On pourra introduire les
constantes P0, T0 et V0.
Mes réponses
a)
Je vous passe les définitions et les unités, on obtient :
b) Je ne vois pas comment intégrer des coefficients qui sont définis à partir de la dérivée partielle de la fonction d'état que je dois justement déterminer en intégrant ces coefficients.
Merci de prendre du temps pour m'aider,
Lantean
Bonjour,
Je ne vois pas trop ce que veux dire intégrer un coefficient. Le texte est bien celui-là ?
D'autre part, sans information supplémentaire, on ne peut intégrer la différentielle dV.
N'y aurait-il pas quelque part, une approximation du type 
et 
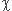constants ?
Merci pour votre réponse,
Il n'y a que ces informations malheureusement.
On propose d'introduire des constantes, mais je ne connais pas d'autres cas que le gaz parfaits, et ici on parle de liquides.
Pour ce qui est de
- vis à vis de la température, c'est juste l'approximation linéaire usuelle
- vis à vis de la pression, l'approximation usuelle que les propriétés des corps condensés dépendent peu de la pression.
Pour ce qui est de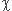
- vis à vis de la pression, c'est juste l'approximation linéaire usuelle
Merci, et désolé de la réponse tardive,
J'ai essayé d'intégrer et ça semble pas trop mal mais dans la question suivante :
c) Que devient cette expression si α(T-T0) et χT (P-P0) sont petits devant 1 ?
Je n'arrive pas à retrouver cette factorisation
Je suis d'accord avec vous, mais on intègre par rapport à la pression et la température... Et je ne vois pas le rapport avec ou
En gros, après approximation, c'est ce que vous devez trouver.
Plutôt que
Je verrai
On voit clairement les deux termes et
Mais il y a peut-être des fautes de frappe.
Cette expression semble super mais je ne vois pas de termes tel que PoX_t qui permettraient de factoriser.
Il y a le V0 dans tous les termes, on peut donc le mettre en facteur.
D'autre part dans votre expression, il y a manifestement des et 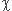oubliés (sinon non homogène, d'où ma "faute de frappe ?", et ensuite les termes en T/T0 et P/P0 doivent être de signe opposé.
Je sens que j'y suis presque mais je crois que mon erreur vient au niveau de l'intégration. Pourriez-vous me montrer la vôtre ?
Si si mais après tu montres que cette quantité est égale à des "termes de pression" et de "température", du coup j'obtiens :
V = -x_t(P-Po) + alpha(T-T0)
Comment obtiens-tu cette expression ? Il y a un V0 dans l'expression de départ, comment peut-il disparaitre ?
côté droite on est d'accord
et côté gauche ?
De plus vous vérifierez que votre équation n'est pas homogène, à droite sans dimension, à gauche un volume.
Je suis bien d'accord, et de toute façon c'était pas V mais ln(V) mea culpa.
On aurait donc ln(V/Vo) = -x_t(P-Po) + alpha(T-T0). Je vois.
Mais le logarithme ne me dit rien qui vaille...
Vous ne connaissez pas le développement limité de ln au voisinage de 1 ?
Sinon, cela se démontre en une ligne.
Autre solution, mais plus physicienne, vous faites l'approximation directement sur l'équation et vous intégrez.
Annuler
connectez vous