Inscription / Connexion Nouveau Sujet
circuit RLC parallèles deux résistances
Bonjour,
Je bute sur mon DM pour la rentrée :
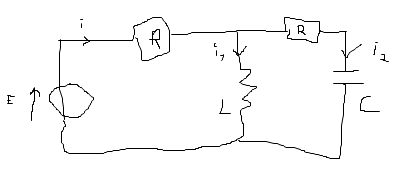
(J'ai dessiné sur paint mon circuit, excusez moi de la qualité désastreuse..)
On appelle U la tension aux bornes du condensateur.
Je dois en déduire l'équation différentielle :
d²U/dt² + [1/(2RC) * (1 + (R²C/L))]*dU/dt + U/2LC = 0
J'ai déjà établie mes lois de Kirchoff telle que :
E = uR + uL
uL=uR+U
i= i1+i2
Je ne vois pas comment commencé..
Merci de votre aide.
Cordialement.
Hello
Je ne vois pas comment commencé..
Préciser la nature de ton générateur de tension?
Si tension alternative, passer aux grandeurs complexe (régime forcé)
E = Ri + L di1/dt
L di1/dt = Ri2 + U
i = i1 + i2
i2 = C dU/dt
---
On élimine i2
E = Ri + L di1/dt
L di1/dt = RC dU/dt + U
i = i1 + C dU/dt
---
On élimine i
E = R(i1 + C dU/dt) + L di1/dt
L di1/dt = RC dU/dt + U
-----
On dérive E = R(i1 + C dU/dt) + L di1/dt par rapport au temps :
0 = R(di1/dt + C d²U/dt²) + L d²i1/dt²
avec di1/dt = RC/L dU/dt + U/L
-->
R(RC/L dU/dt + U/L + C d²U/dt²) + L (RC/L d²U/dt² + dU/dt * 1/L) = 0
R²C/L dU/dt + U * R/L + RC d²U/dt² + RC d²U/dt² + dU/dt = 0
R²C/L dU/dt + U * R/L + 2.RC d²U/dt² + dU/dt = 0
2.RC d²U/dt² + (1 + R²C/L) dU/dt + U * R/L = 0
d²U/dt² + [(1 + R²C/L)/(2RC)] dU/dt + U/(2LC) = 0
-----
A savoir refaire ... bien entendu.

Et j'aurai une dernière question, comment dois je commencer pour trouver la solution exacte u(t) en fonction des paramètres w0 et Q ?
Merci d'avance !
d²U/dt² + [(1 + R²C/L)/(2RC)] dU/dt + U/(2LC) = 0
d²U/dt² + wo/Q dU/dt + wo².U = 0
--> wo² = 1/(2LC)
et :
wo/Q = (1 + R²C/L)/(2RC)
Q = 2RC.wo/(1 + R²C/L)
Q = 2RLC.wo/(L + R²C)
Q = (2RLC.* 1/(V(2LC))) /(L + R²C) (Avec V pour racine carrée)
Q = (R * V(2LC))/(L + R²C)
-----
d²U/dt² + wo/Q dU/dt + wo².U = 0
p² + wo/Q . p + wo² = 0
p = [-(wo/Q) +/- (wo²/Q² - 4.wo²)^(1/2)]/2
p = [-(wo/Q) +/- wo.(1/Q² - 4)^(1/2)]/2
p = [-(wo/Q) +/- (wo/Q).(1 - 4Q²)^(1/2)]/2
Les solutions dépendent du signe de (1 - 4Q²)
a)
Si (1 - 4Q²) < 0 (donc Q > 1/2), alors :
p = [-(wo/Q) +/- j.(wo/Q).RC(4Q²-1)]/2
U(t) = (e^(-wo/(2Q))*t) * [A * sin(t * (wo/(2Q)) . RC(4Q²-1)) + B * cos(t * (wo/(2Q)) . RC(4Q²-1))]
A et B sont des constante à déterminer à partir des conditions initiales.
b)
Si (1 - 4Q²) < 0 (donc Q < 1/2), alors :
U(t) = ...
c)
Si (1 - 4Q²) = 0 (donc Q = 1/2), alors :
U(t) = ...
-----
Sauf distraction (rien vérifié). 


