Niveau iut

Circuit RLC parallèle forme canonique

Posté par
AeRoLiNeR 13-03-15 à 19:00

Bonjour,

Je but sur un exercice sur les systèmes du 2nd ordre.

Voici l'énoncé :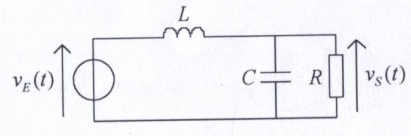

Circuit RLC parallèle forme canonique

** image supprimée **

** énoncé effacé ; image laissée **

J'ai trouvé H = Zeq/(Zeq+jL)
Ensuite je développe avec Zeq = (zC.R)/(zC+R) mais je n'arrive pas à mettre H sous forme canonique pour identifier H0, m et 0

Je vous remercie par avance pour votre aide.

Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum

Posté par re : Circuit RLC parallèle forme canonique 13-03-15 à 19:13

Bonjour,
Montre comment tu fais. On corrigera.

Posté par re : Circuit RLC parallèle forme canonique 13-03-15 à 21:21

Voici l'énoncé :

Citation :
1) Déterminer la fonction de transfert H = VS/VE en fonction de R, L et C.

2) Mettre H sous forme canonique $\Large H=\frac{H0}{1+2.m.j.\frac{w}{w0}+(j.\frac{w}{w0})²}$ où :
- H0 désigne le gain statique,
- m désigne le coefficient d'amortissement,
- w0 désigne la pulsation propre du système

On exprimera les trois coefficients H0, m et w0 en fonction de R, L et C

J'applique le pont diviseur de tension :

$\Large H=\frac{zeq}{zeq+Zl}$

Je divise tout par zeq mais je me demande si c'est la bonne méthode ?

$\Large H=\frac{1}{1+\frac{Zl}{zeq}}$

avec zeq = (R/jcw)/((1/jcw)+R)

Au final j'arrive à :

$\Large H=\frac{1}{1+\frac{-RCw+j}{-LRw}}$

Je suis sur le bon chemin ou je m'égare complètement ?

Posté par re : Circuit RLC parallèle forme canonique 14-03-15 à 01:15

Bonsoir,

$\underline{Z_P}=\dfrac{R}{1+j\omega CR}$

$\underline{Z}=\underline{Z_L}+\underline{Z_P}=j\omega L+\dfrac{R}{1+j\omega CR}$

$\underline{H}=\dfrac{\underline{V_S}}{\underline{V_E}}=\dfrac{\underline{Z_P}}{\underline{Z_L}+\underline{Z_P}}=\dfrac{R}{R-\omega^2 LRC+j\omega L}=\dfrac{1}{1-\omega^2LC+\dfrac{j\omega L}{R}}=\dfrac{1}{1+(\dfrac{j\omega}{\omega_0})^2+\dfrac{j\omega L}{R}}$

$\omega_0^2=\dfrac{1}{LC}$

$\dfrac{2m}{\omega_0}=\dfrac{L}{R}$

Sauf erreur de recopie