Inscription / Connexion Nouveau Sujet
Circuit RLC complexe
Bonjour, bonsoir ! alors voila j'ai quelque difficultés pour 3 questions :
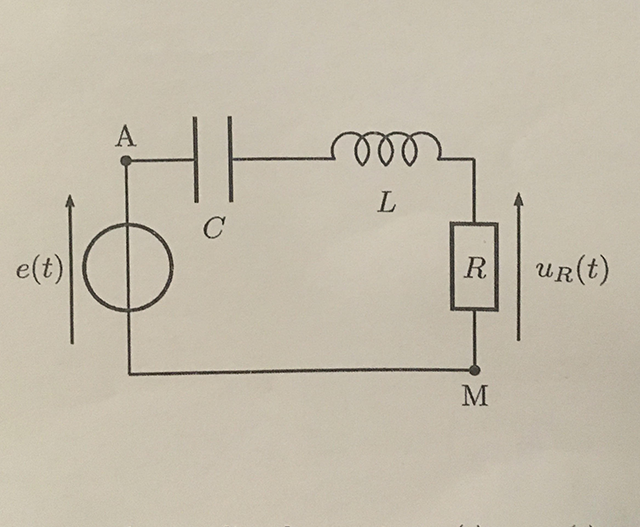
On considère le circuit RLC série representée ci-dessous, alimenté par un générateur de tension sinusoidale e(t)=Ecost( t), le générateur de tension et le condensateur sont supposés idéaux, la bobine est supposée idéale dans un premier temps, avant que l'on raffine ce modèle, on donne R=20
t), le générateur de tension et le condensateur sont supposés idéaux, la bobine est supposée idéale dans un premier temps, avant que l'on raffine ce modèle, on donne R=20 et C=10
et C=10 F
F
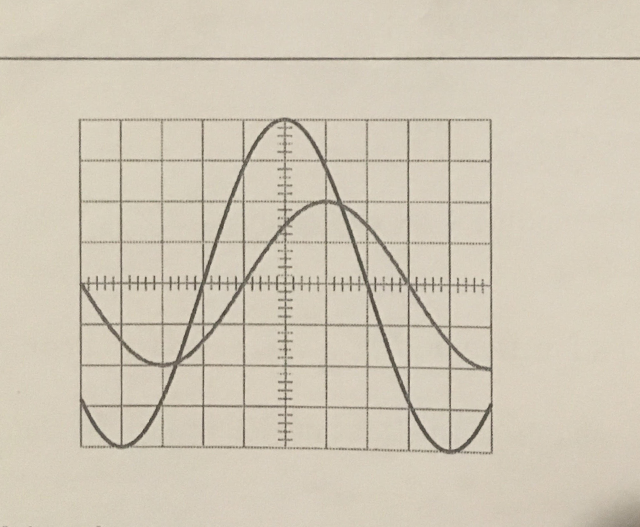
Un oscilloscope permet de visualiser les tensions e(t) et Ur(t), avec les calibres 0.5V/div verticalement et pour les deux voies 0.5 s/div horizontalement, les courbes sont obtenus dans un graphique
s/div horizontalement, les courbes sont obtenus dans un graphique
1) Déterminer l'impédance complexe équivalente ZAM(j ) du dipole AM correspondant à l'association série condensateur, bobine et résistance
) du dipole AM correspondant à l'association série condensateur, bobine et résistance
On a que Z=R+jL +1/(jC
+1/(jC )
)
2) en déduire les expressions de l'amplitude URm( ) de Ur(t) et de l'avance de phase
) de Ur(t) et de l'avance de phase  (
( ) de Ur(t) sur e(t)
) de Ur(t) sur e(t)
celle j'ai des soucis, mon probleme c'est que je n'ai pas l'idée de la forme que la question veut et je ne comprend pas l'intérieur des fonctions par exemple avec des oméga puis des t dans les parenthèses
3) Montrer que la tension Ur(t) est sujette à un phénomène de résonance pour une pulsation  r que l'on précisera, Que vaut
r que l'on précisera, Que vaut  (
( r)
r)
Meme problème
Merci de votre aide !
Bonjour
OK pour ton expression de l'impédance complexe du circuit. Pour uR, tu peux considérer que l'association série RLC se comporte en diviseur de tension. Tu obtiens ainsi très simplement l'expression de uR en fonction de e, Z et R. L'amplitude de uR correspond au module du complexe associé...
La phase de uR est l'argument du complexe associé...
Revois si nécessaire ton cours sur l'usage des complexes en régime sinusoïdal.
Merci de votre réponse ! Je vais y jeter un coup d'oeil, mais concretement mon phi et mon URm c'est juste des etudes d'amplitude et d'angle avec les arctan, mais l'interieur de ces fonctions avec omega ou t c'est ça qui me perturbe, concretement y'a rien qui change alors pour expressions ?
L'intérêt des deux expressions (celles de URm et  ) est de pouvoir étudier théoriquement l'influence de la fréquence, et donc de la pulsation
) est de pouvoir étudier théoriquement l'influence de la fréquence, et donc de la pulsation  ,sur ces deux grandeurs (amplitude et phase initiale) qui caractérisent la tension instantanée uR(t). Cela va te conduire à parler de résonance (question 3).
,sur ces deux grandeurs (amplitude et phase initiale) qui caractérisent la tension instantanée uR(t). Cela va te conduire à parler de résonance (question 3).
Tu as oublié au "carré" dans l'expression de URm
Pour justifier la résonance, il n'est pas nécessaire de faire un calcul fastidieux de dérivée. Sachant que le numérateur est une constante positive, URm présente un maximum quand le dénominateur présente un minimum ; le minimum d'un carré est la valeur nulle... Tu as logiquement étudié en cours la notion de résonance d'intensité pour un circuit RLC série. L'étude est très analogue puisque uR=R.i
Du coup c'est tous le denominateur qui vaudra 1 ? Puisqu'on ne peut pas diviser par 0, et aussi je pense que j'aurai du factoriser par R
Le minimum de vaut évidemment
et est obtenu pour une pulsation telle que :
. Tu n'as pas étudié en cours la notion de résonance d'intensité ?
Si si je l'ai étudié ! c'est R2 pour la formule que j'ai écris et 1 si on factorise par R, jlavais écris sur ma feuille
Parcontre je ne sais pas comment on fait pour identifier Ur(t) et e(t) sur le graphique ...
Relis mon message du 04-01-19 à 12:43.
A propos des courbes : comme indiqué l'échelle des temps (axe horizontal) est commune aux deux courbes . En est-il de même pour l'axe vertical des tensions ? Si oui, la bobine ne peut pas être modélisée par une inductance pure mais j'anticipe peut-être la suite du problème...
ça marche ! Oui vous avez une très bonne intuition  ! mais bon je vais essayer de faire la suite tout seule, merci de votre aide
! mais bon je vais essayer de faire la suite tout seule, merci de votre aide
Du coup j'ai pas vraiment trouver ce que je cherchais exactement sur le lien mais je pense que la courbe la plus grande en amplitude c'est e(t), et que Ur(t) c'est l'autre à cause de la résistance
Oui vous avez une très bonne intuition
Cela n'a rien à voir avec l'intuition. Le décalage temporel entre les deux courbes est de une division alors que la période correspond à 8 divisions. Le déphasage entre les deux tensions instantanées vaut donc
je pense que la courbe la plus grande en amplitude c'est e(t),
Cela se démontre facilement à partir des formules écrites précédemment.

 (R2+(Lw-1/Cw))) et jai que
(R2+(Lw-1/Cw))) et jai que 
