Inscription / Connexion Nouveau Sujet
Circuit RL
Bonsoir,
dans un exercice corrigé en cours,je n'ai pas tout compris au corrigé et j'aurai voulu éclaircir certains points.
Voici l'exo:
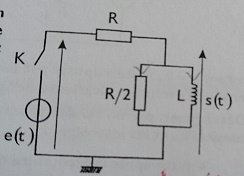
Le circuit ci-contre est alimenté par un générateur de force électromotrice constante E.
A l'instant t=0,on ferme l'interrupteur K.
1a)La tension et le courant sont-ils à priori continu en t=0?
Commenter physiquement ,puis exprimer s(t=0+).
b)déterminer le comportement asymptotique s(
 ).
).
2)établir l'équa.diff vérifié par s(t).
3)En fonction de L et R exprimer le temps t0 tel que s(t0)=s(t=0+)/10.
Et voici les réponses:
1)a)Le courant dans une bobine est toujours continu,mais s(t)=Ur=R/2.i1=UL peut être discontinu car i1=iR peut être discontinu.
De même i(t) peut l'être(j'ai compris ça).
b)t
 (régime permanent)
(régime permanent)
s(
 )=?...impédance
)=?...impédance
La bobine équivaut à un fil(ZL=jlw) (je sais pas pourquoi on parle de complexe et d'impédance là...).
2)J'épargne les calculs...on trouve s(t)=(E/3)*e-t/Tau,Tau=R/3L jusque là ça va,(Tau c'est de la forme R/L pour 1 circuit RL,c'est normal).
Cependant pour le 3)On trouve S(t0)=(E/3)*(1/10) et Tau=3L/R,mais pourquoi le Tau du 3 est différent à celui du 2?
2)J'épargne les calculs...on trouve s(t)=(E/3)*e-t/Tau,Tau=R/3L jusque là ça va
Ben non cela ne va pas. R/(3L) n'a pas les dimensions d'un temps ... mais bien les dimension de l'inverse d'un temps ---> C'est là qu'est l'os.
s = R/2 * i2
s = L di3/dt
E - R.i1 = s
i1 = i2 + i3
On élimine i2
s = L di3/dt
E - R.i1 = s
i1 = 2s/R + i3
On élimine i1
s = L di3/dt
E - R.(2s/R + i3) = s ---> i3 = ((E-s) - 2s)/R = (E - 3s)/R
s = L d((E - 3s)/R)/dt
s = L/R * (-3.ds/dt)
ds/dt + (R/(3L)).s = 0
s(t) = K.e^(-R/(3L) * t)
Avec s(0) = E * (R/2)/(3R/2) = E/3 -->
s(t) = (E/3) * e^(-R/(3L) * t)
A comparer avec s(t) = (E/3) * e^(-t/Tau)
---> Tau = 3L/R (et pas ce que tu as écrit dans la question 2)

Ouf,ça me rassure que les Tau soit pareil,peut être que j'ai mal recopier.
Merci pour ton aide J-P,mais pour le 1b),on utilise l'impédance ZL(en complexe) pour répondre,mais pourquoi?
Ouf,ça me rassure que les Tau soit pareil,peut être que j'ai mal recopier.
Ah oui je comprend mon erreur pour Tau,Tau=L/R pour un circuit RL,ma prof m'a dit l'inverse,bref.
La bobine équivaut à un fil(ZL=jlw) (je sais pas pourquoi on parle de complexe et d'impédance là...).
UL = L.di/dt
Or en régime établi dans le circuit utilisé, le courant tend (pour t --> +oo) vers un constante continue et donc le variation de courant tend vers 0 (pour t --> +oo)
Donc pour t--> +oo, avec UL = L.di/dT et di/dt --> 0, on a UL --> 0
La tension UL aux bornes de la bobine tend vers 0, la bobine se comporte donc comme un simple fil (un court-circuit) pour t --> +oo, on a ZL = 0
----
Une autre approche est de dire :
Pour t --> +oo, le courant tend vers une constante continue, soit donc comme un courant sinusoïdal qui aurait une fréquence nulle.
Or, en sinusoïdal, l'impédance d'une bobine est ZL = jwL.
Si la fréquence f est nulle, alors w est nulle aussi (puisque w = 2.Pi.f)
Donc pour t --> +oo, dans le circuit considéré, zL --> 0
-----
Sauf distraction.



