Inscription / Connexion Nouveau Sujet
Circuit RC: équation vérifiée par la charge q(t).
Bonjour, Je suis un debutant en electronique et j'ai besoin de votre aide dans cet exercice .
Notre professeur nous a dicté l'enoncé de l'exercice exactement comme ainsi :
-Déterminer l'équation différentielle en fonction de la charge q(t) du condensateur, et sa solution en état de charge
-Déterminer l'expression de la constante de temps
Il nous a même fait une remarque que c'est pas évident.
Ben, selon ma solution, le résultat que j'ai trouvé est :
- q(t)=CE*[(1-exp(-1/R1C)] ,
- Tau= R(eq)*C(eq)
puisque U=Uc+Ur1=Ur2 et R=U/i
on trouve que Tau= [(Uc+Ur1)/i1]*C=R1*C , puisque Uc/i1=Rc=0
Mais c'est très simple pour qq chose de « pas evident »
Ce qui veut dire que c'est faux.
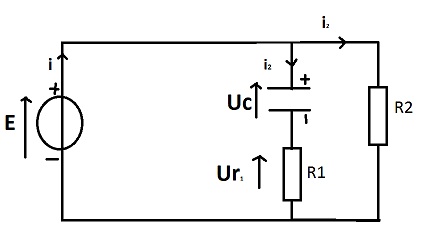
Attention, ton expression de q(t) ne dépend pas de t comme tu l'as écrite ... Je suppose que c'est une distraction.
Ton schéma note i2 pour 2 courants différents ... Je suppose que c'est i1 dans la branche avec le C.
---------------------
E = R1.i1 + Uc
i1 = C.dUc*dt
E = R1.C.dUc*dt + Uc
q = C.Uc
Uc = q/C
E = R1.dq*dt + q/C
dq/dt + q/(R1.C) = E/R1
-----
q(t) = A.e^(-t/(R1.C)) + C.E
Si q(0) = Qo, alors :
A + C.E = Qo
A = Qo - CE
q(t) = (Qo - CE).e^(-t/(R1.C)) + C.E
q(t) = Qo.e^(-t/(R1.C)) + C.E.(1 - e^(-t/(R1.C)))
Et dans le cas particulier où Qo = 0, on a : q(t) = C.E.(1 - e^(-t/(R1.C)))
-----
tau = R1.C (à la charge)
Annuler
connectez vous