Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Circuit R1L et R2C

Posté par
Jean469 04-10-15 à 08:13

Bonjour,j'ai pas trop mal commencer un exo sur les circuit mais ma rédaction est un peu brouillon,voilà pourquoi j'aurai voulu qu'on me dise quelles erreurs j'aurai pu faire.

L'énoncé est le suivant:

On considère un circuit R1L série placé en parallèle à un circuit R2C série.
L'ensemble est alimenté par une source de tension idéale E par l'intermédiaire d'un interrupteur.

1)Réaliser le montage.
2)Le condensateur est initialement déchargé .

A t=0,on ferme l'interrupteur.
Estimer i_L et i_C  puis exprimer i(t) le courant débité par la source.

3)calculer le temps t1 pour lequel i(t) est minimum.
Et comme on peut le voir sur mon schéma: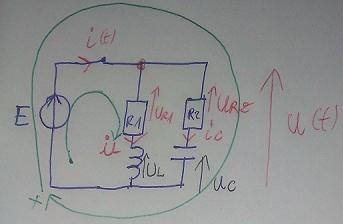

Circuit R1L et R2C
,i(t)=i_L+i_C.

Ensuite i_c=C.duc/dt et i_L=CduL/dt (je sais pas si il vaut mieux écrire u_l et u_c au lieu de "u" par

contre).
Enfin selon mon schéma,u(t)=Ldi/dt+Ri,donc i(t)=

i(t)=\frac{\frac{C.d(L\frac{Ldi}{dt}+Ri)}{dt}}{R}+même chose

=\frac{\frac{2C.d(L\frac{Ldi}{dt}+Ri)}{dt}}{R} avec i(t)=U(t)/R.
Mais pour la question 3 par contre j'aurai besoin d'aide.

***Image recadrée***

Posté par
vanoisere : Circuit R1L et R2C 04-10-15 à 10:02

Bonjour,
Une fois l'interrupteur fermé, u(t) = E quel que soit t ! Les trois branches sont en parallèles et le générateur de tension est idéal ! La situation est simple !

Posté par
Jean469re : Circuit R1L et R2C 04-10-15 à 15:16

Ah mince donc ce que j'ai écrit est faux!
Alors ça veut dire que pour t1,on peut dire que i(t1)=u(t1)/R,mais je vais tout reprendre vu les nouvelles infos que tu m'a donné.
Merci

Posté par
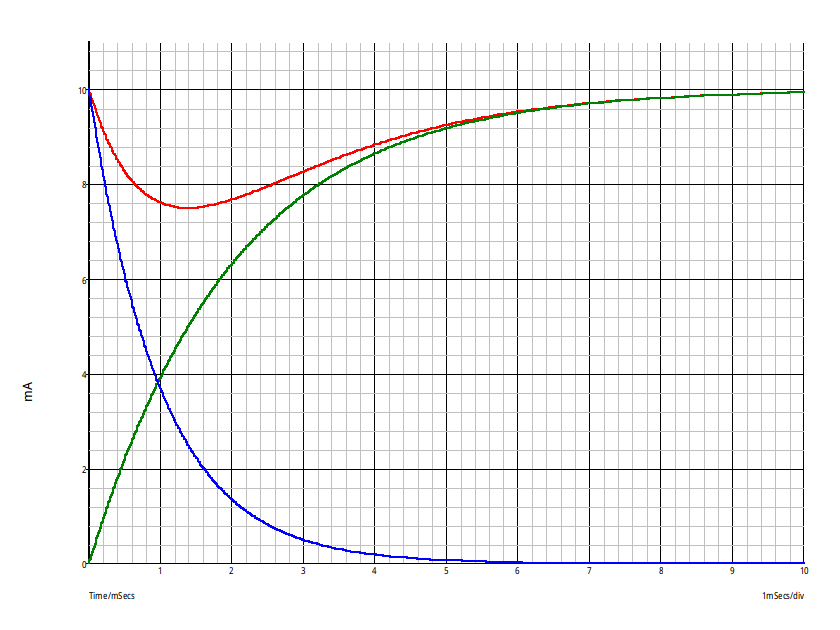
vanoisere : Circuit R1L et R2C 04-10-15 à 23:28

Cela t'aidera peut-être : voici les trois courbes i1(t), i2(t) et i(t). Volontairement je n'ai pas mis de légende : à toi de les identifier !
J'ai choisi les valeurs arbitraires suivantes : E = 1V ; R1 = R2 = 100 ; L = 200mH ; C = 10µF

Circuit R1L et R2C

Posté par
Jean469re : Circuit R1L et R2C 10-10-15 à 16:15

Désolé de répondre si tard!!!
Oui j'avais vu ton message mais je comptais y répondre plus tard procrastiné.
Oui ça m'a été utile quand même,j'étais mal partie depuis le début!
Vraiment désolé pour le retard.
Tu vas bien sinon?

Posté par
Jean469re : Circuit R1L et R2C 23-01-16 à 14:22

Salut,j'ai refais bien cet exo(énoncé en haut). dont le schéma est en bas,et voici ce que j'ai pu écrire pour l'instant(c'est bon un prof me l'a dit):
2) E = R1.iL + L.diL/dt \\ iL = K.e^(-R1/L * t) + E/R1 \\ iL(0) = 0 --> K = -E/R1 \\ \\ iL(t) = E/R1 * (1 - e^(-R1/L * t)) \\ \\ E = R2.ic + Uc \\ avec ic = C.dUc/dt \\ \\ R2.ic + dUc/dt = 0 \\ R2.dic/dt + ic/C = 0 \\ \\ ic = K'.e^(-t/(RC)) \\ ic(0) = E/R2 --> K' = E/R2 \\ \\ ic(t) = E/R2 * e^(-t/(R2.C)) \\ 3) a) i(t) = ic(t) + iL(t) \\ i(t) = E/R2 * e^(-t/(R2.C)) + E/R1 * (1 - e^(-R1/L * t)) \\
Le schéma du 1) est en bas quand à lui.
Mais j'aurai besoin d'aide pour le 3b) si possible:
3)b)calculer le temps t1 pour lequel i(t) est minimum.
A l'aide de t1 et des limites,tracer i(t) en supposant que R1>R2.

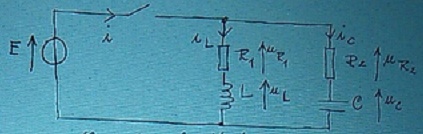
Circuit R1L et R2C

Posté par
Jean469re : Circuit R1L et R2C 23-01-16 à 14:51

Up

Posté par
vanoisere : Circuit R1L et R2C 23-01-16 à 16:52

Bonjour,
La courbe i(t) que tu dois étudier est celle que j'ai tracé en rouge. Cela te permettra de vérifier tes résultats.
Pour la date correspondant au minimum de i(t), je ne vois pas plus simple qu'un calcul de dérivée : le minimum sera obtenu pour di(t)/dt = 0

Posté par
Jean469re : Circuit R1L et R2C 23-01-16 à 19:40

Ok,merci  j'obtient donc cela:

***Proposition scannée supprimée***

***Tu peux poster un schéma manuscrit, mais l'énoncé ou tes propositions doivent être recopiées***

Posté par
vanoisere : Circuit R1L et R2C 23-01-16 à 22:56

Bonsoir,
Ton calcul semble bien commencé mais je ne vois pas le résultat final. Voici ce que j'obtiens avec l'application numérique correspondant à la simulation précédente. Il y a bien cohérence !

\begin{cases} \\ i_{1}=\frac{E}{R_{1}}\left(1-e^{-\frac{t}{\tau_{1}}}\right) & avec\quad:\quad\tau_{1}=\frac{L}{R_{1}}\\ \\ i_{2}=\frac{E}{R_{2}}\cdot e^{-\frac{t}{\tau_{2}}} & avec\quad:\quad\tau_{2}=R_{2}C\\ \\ i=i_{1}+i_{2} & \frac{di}{dt}=\frac{di_{1}}{dt}+\frac{di_{2}}{dt}\\ \\ \frac{di}{dt}=\frac{E}{R_{1}\tau_{1}}e^{-\frac{t}{\tau_{1}}}-\frac{E}{R_{2}\tau_{2}}e^{-\frac{t}{\tau_{2}}} & \frac{di}{dt}=0\\ \\ \frac{e^{-\frac{t}{\tau_{1}}}}{R_{1}\tau_{1}}=\frac{e^{-\frac{t}{\tau_{2}}}}{R_{2}\tau_{2}} & \frac{e^{-\frac{t}{\tau_{1}}}}{e^{-\frac{t}{\tau_{2}}}}=\frac{R_{1}\tau_{1}}{R_{2}\tau_{2}}\\ \\ \text{passage aux logarithmes :} & \frac{t}{\tau_{2}}-\frac{t}{\tau_{1}}=\ln\left(\frac{R_{1}\tau_{1}}{R_{2}\tau_{2}}\right)\\ \\ t=\frac{\tau_{1}\tau_{2}}{\tau_{1}-\tau_{2}}\ln\left(\frac{R_{1}\tau_{1}}{R_{2}\tau_{2}}\right) & \boxed{t=\frac{LR_{2}C}{L-R_{1}R_{2}C}\ln\left(\frac{L}{R_{2}^{2}\cdot C}\right)}\\ \\ R_{1}=R_{2}=100\Omega;L=0,20H;C=10\mu F & \text{date du minimum de i : \ensuremath{\boxed{t=1,39ms}}} \\ \end{cases}
On remarque que l'existence d'un minimum n'est possible que si :

L>R_{1}R_{2}C

Posté par
Jean469re : Circuit R1L et R2C 24-01-16 à 14:49

Bonjour vanoise,merci pour ton aide mon ami!
J'ai trouvé la même chose que toi sauf que j'ai t=LR2C/(-L+R1.R2C).Ln(L/R2²C).
J'ai du faire une erreur.

Posté par
vanoisere : Circuit R1L et R2C 24-01-16 à 15:06

Bonjour,
Il m'arrive de commettre des étourderies de calcul mais la concordance entre mon calcul et la simulation informatique postée le 4/10 m'incite à soupçonner une erreur de signe de ta part : ton calcul conduirait, avec les valeurs numériques de la simulation, à une date négative, ce qui n'a pas de sens !

Posté par
Jean469re : Circuit R1L et R2C 24-01-16 à 17:44

Effectivement!
Une erreur de signe,c'est si vite arrivé!


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !