Inscription / Connexion Nouveau Sujet
Circuit équivalent à un quartz piezoelectrique
Bonsoir,
J'ai besoin d'aide pour un DM à rendre qui traite d'un circuit équivalent à un quartz piézoélectrique. Je ne sais pas comment procéder pour la première question et j'aurais besoin d'un peu d'aide. J'avais essayé de calculer l'impédance complexe du circuit mais je n'aboutis à rien et je ne suis pas sur que cela soit nécessaire.
La première question est : Calculer les pulsations pour lesquelles le courant dans le circuit principal est infini ou nul
Merci d'avance pour votre aide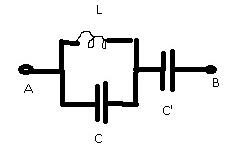
***Image recadrée***
Bonsoir,
Ton idée de calculer l'impédance complexe est excellente.
Ensuite : que se passe-t-il si le module de l'impédance complexe tend vers zéro ?
Que se passe-t-il si le module de l'impédance complexe tend vers l'infini ?
Bonsoir,
Lorsque je calcule l'impédance complexe je trouve (L/C)/(jLW+1/jCW) + 1/jC'W donc en simplifiant j(LCW+LCW^2 -1)/C-LC^2W^2
après j'ai fais la loi de pouillet pour trouver le courant complexe et en calculant le module je trouve E(C-LC^2W^2)/LCW+LCW^2 -1
Donc du coup après je ne sais pas comment faire
Bonsoir,
A priori, si tu obtiens une expression du module du complexe associé à l'intensité de la forme :
I = 0 si A( )=0 avec B(
)=0 avec B( )
) 0 ;
0 ;
I
 pour B(
pour B( )=0 avec A(
)=0 avec A( )
) 0
0
Evidemment, en pratique, l'intensité ne peut pas tendre vers l'infinie : la résistance d'une bobine n'est jamais nulle et les générateurs de tension usuels ont une résistance interne non nulle.
Logiquement je pense que je devrais trouver et pour le deuxième
Pour le premier je trouve bien ça mais pas pour le deuxième
Si vous pouviez m'aider
oubli mon message précédent, j'ai oublié un terme à la dernière ligne ; voici le rectificatif ; ton corrigé à tord...
Merci. Je n'ai pas de corrigés. C'était juste une déduction des questions qui suivent dans mon exercice. Merci à toi en tout cas
Z = 1/(jwC') + (jwL/(jwC))/(jwL + 1/(jwC))
Z = 1/(jwC') + jwL/(1-w²LC)
Z = [(1-w²LC) - w²LC']/[jwC(1-w²LC)]
Z = [1-w²L(C+C')]/[jwC(1-w²LC)]
Et donc Z = 0 si 1-w²L(C+C') = 0, donc pour w = RacineCarrée[1/(L(C+C'))]
et Z --> oo si wC(1-w²LC) = 0, donc pour w = 0 ou w = RacineCarrée[1/(LC)]
Quant au courant dans le "circuit principal", il dépend évidemment aussi du reste du circuit ... sauf pour w = 0 rad/s ou w = RacineCarrée[1/(LC)] pour lesquels i = 0
Sauf distraction. 
En écrivant l'impédance complexe en fonction de ces valeurs je trouve
[1-(W^2/Wo^2)]/jC'W(1-(W^2/Wi^2))
Ensuite il faut que je calcule la variation d'impédance lorsque la fréquence varie légèrement. Pour w=wi l'impédance du quartz est très faible. J'ai essayé de calculer dZ/dw mais celà ne m'aide pas. On me dit également d'exprimer le module de deltaZ/deltaF
Bonjour,
Sans énoncé complet, difficile de t'aider. Il s'agit peut-être d'effectuer un développement limité de Taylor au voisinage de la pulsation étudiée (wi ???). Ce type de développement passe par le calcul d'une dérivée.
Voici la question :
Pour w=wi, l'impédance du quartz n'est pas nulle, mais très faible. On fait osciller le quartz à la fréquence Fi. Calculer la variation d'impédance lorsque la fréquence varie légèrement, la tension d'alimentation restant constante.
Aide : calculer [dZ/dw]w=wi puis exprimer
Montrer que
C'est donc bien ce que j'avais "deviné" !
Développement de Taylor limité à l'ordre 1 au voisinage de  =
= i :
i :
La dérivée de Z par rapport à  est calculée pour le cas particulier :
est calculée pour le cas particulier :  =
= i
i
J'ai vérifié : on obtient bien le résultat proposé.
Il n'y a pas de suite : toute la difficulté consiste à calculer la dérivée :
voici ce que j'ai obtenu :
Dans le cas particulier :
Cette dérivée vaut :
Tu n'as plus qu'à refaire ces calculs et conclure !
J'ai une question sur un exercice différent qui est sur une adaptation d'impédance.
J'ai calculé la puissance d'un circuit constitué d'un generateur de tension sinusoidale de resistance interne r qui alimente une résistance variable R.
Je trouve que la puissance reçue par R est la suivante : P=tex]E^2\frac{R}{(R+r)^2}[/tex]
J'ai trouvé que Pour R=r la puissance fournie par le générateur est maximale
On dit qu'il y a adaptation d'impédance donc si R=r. Si ceci n'est pas vérifiée on intercale un dipole adaptateur (constitué d'éléments passifs) entre le générateur et la résistance de charge R.
L'impédance d'entrée Ze complexe est égale à :
Donc pour que Rg=Ze il faut que L=
et C=
La dernière question est de calculer la puissance transférée à la charge Ru et de comparer avec la valeur transféré directement sans quadripôle adaptateur et conclure.
J'ai dit que P=
et que Un récepteur reçoit la puissance max si son impédance est le conjugué de l'impédance du générateur de Thevenin qui l'alimente mais je ne vois pas quoi faire en plus. Si vous pouviez m'aider merci d'avance
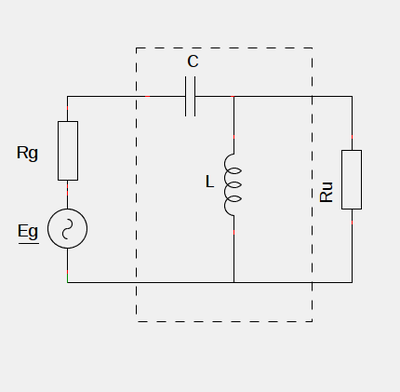
En présence de l'adaptateur, le résultat s'obtient sans calcul sachant que la puissance moyenne (ou active) consommée par L et par C est nulle.
Le générateur fournie la même puissance que s'il était reliée à une résistance égale à sa résistance interne Rg puisque l'ensemble {Ru, quadripôle adaptateur} est vu du générateur comme une résistance Rg. Le circuit est équivalent, vue du générateur, à une fem Eg alimentant une résistance 2Rg. Le générateur est parcourue par un courant d'intensité efficace I = E/(2Rg). Il fournie donc la puissance moyenne :
; 50% de cette puissance est consommée par effet Joule par le générateur. La puissance restante (50%) est transmise à la résistance Ru puisque le quadripôle adaptateur n'en consomme pas en moyenne. (les lettres E et I désignent les valeurs efficaces). Donc : Pu=E2/(4Rg)
Sans dipôle adaptateur : loi de Pouilet : I = E/(Ru+Rg) puis loi de Joule : Pu=Ru.I2.
Formule utilisée dès le début.


