Inscription / Connexion Nouveau Sujet
Circuit,équation différentielle du second ordre.
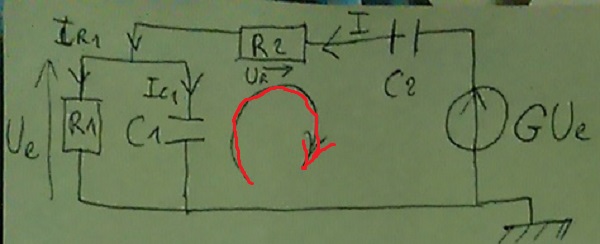
Bonjour,j'ai besoin d'aide pour cet exercice(schéma en bas): Ils me demandent pour la question 1:
1) Trouver l'équation du second ordre vérifié par Ue.
2) Pour une valeur particulière de G, G0, la solution obtenue correspond à un régime sinusoïdal.
Exprimez G0 et la pulsation w0(omega) du signal Ue (t).
3) R1 = R2 = 1,5kΩ, C1
= C2 = 0,1μF calculer G0 et w0.
Et ma réponse est:
. (c'est la LDN)
Puis la LDM donne:.
D'ou
Et on en déduit que .
Puis en 2) j'aurai envie de dire que vu que c'est une équation du second degré,on calcul le discriminant delta,mais je vois dans mon cours que si On a
.
Donc si G=3 On a tous ce qu'il reste=0(équa générale sans second membre,Si G = 3
donc: R2²C2².d²Ue / dt + Ue = 0. ) et la solution c'est
.
Pour trouver w :condition initiales à t=0 U(t=0)=0 donc Ue=A.cos0+B.sin0=0=>A=0 ensuite le reste je ne sais point.
Bonjour,
Je n'ai pas pris le temps de vérifier tes calculs. Si tu obtiens effectivement une équation différentielle du second ordre il faut l'écrire sous la forme :
 o est la pulsation propre.
o est la pulsation propre.
Le cas particulier correspondant à une solution sinusoïdale correspond à  = 0
= 0
La solution est alors de la forme :
Calculs vérifiés : OK pour l'équation différentielle.
La solution sinusoïdale correspond bien à G = 3. La pulsation est égale alors à la pulsation propre :
Dans ce que tu as copié comme énoncé, rien ne permet d'obtenir l'amplitude Uem et la phase initiale 
j'ai dis que w0=1 car j'ai R2²C2².d²Ue / dt + 1.Ue = 0.
Mais bon si tu trouve autre chose pour w0 tu dois avoir raison.
(1/(c2.R1))Ue+(c1/c2+R2/R1+1-G).dUe/dt+R2.C1.d^2Ue/dt^2=0..
Cette ligne est correcte. Pour la suite, en suivant la méthode que je t'ai proposée, tu dois logiquement obtenir l'expression de la pulsation propre que je t'ai indiquée à 15h24.

 .
.
